Análisis de sensibilidad con el Método de Montecarlo
Una vez que tenemos un modelo de simulación construido, probado e incluso calibrado, queremos saber cómo responde ante cambios en los parámetros utilizados. Es decir ¿cuán sensibles resultan los resultados del modelo a los cambios en esos parámetros sobre los cuales tenemos dudas?. Este análisis posterior a la construcción y ajuste del modelo se conoce como Análisis de Sensibilidad.
Si tenemos un modelo con parámetros que son variables continuas distribuidas en forma normal, podemos preguntarnos si será necesario ejecutar el programa un número infinito de veces, cambiando cada vez los valores. Esto es imposible de llevar a la práctica. Por suerte la respuesta a esa pregunta es negativa. Lo que si se puede hacer, con menos costo y en tiempos razonables es simular el proceso un gran número de veces (aunque finito) adoptando cada vez valores diferentes en los parámetros. A la técnica de simular un proceso que contiene elementos aleatorios repitiendo el proceso una y otra vez para ver cómo se comporta se le llama Método de Montecarlo
.
Consideremos la siguiente situación: un fabricante de cervezas se encuentra con problemas para programar su producción. No conoce su participación exacta en el mercado, lo afecta la estacionalidad del consumo, desconoce la capacidad máxima de consumo del mercado al cual dirige su producto. Encarga un estudio, y le informan que el máximo consumo ronda el 1.000.000 de litros diarios, y que un estudio sobre 500 personas que probaron la bebida comparando con su principal competidor, 350 han elegido su producto. Sus asesores le dicen que sería adecuado formular un modelo de simulación sobre el cual se haga un análisis de sensibilidad considerando que la variable “consumo” se comporta según una Distribución Binomial. Así que un muy sencillo modelo de simulación dinámica, que considere una producción, un nivel de stock y un consumo le darán una primera aproximación rápida de cómo programar su producción. Este mismo modelo podrá luego ir completándose a efectos de considerar otras variables que afecten el consumo (estacionalidad, poder adquisitivo, aparición de nuevos productos, búsqueda de nuevos mercados...).
Una vez que se ha construido y probado el modelo, la elección de la herramienta de Análisis de Sensibilidad abre un cuadro que requiere definir algunos datos, dependiendo de la distribución que se elija. Las opciones son varias, si bien las más comunes son la distribución uniforme, que asigna a todos los valores igual probabilidad, y la distribución normal. En este ejemplo hemos elegido la binomial. Seleccionamos como variables aleatorias las que creemos que influyen de forma más decisiva en el comportamiento del sistema. Donde debemos poner mayor cuidado es cuando elegimos la distribución. En el caso de la binomial hemos de definir 6 parámetros. Se nos pide un valor mínimo, uno máximo, una probabilidad, el número de simulaciones, la media y la desviación estándar. Los dos primeros tienen que ver con la situación real, y pueden elegirse aprovechando los datos del ensayo. Los cuatro últimos tienen que ver con la distribución y para nuestro ejemplo del fabricante de cerveza serían 0.7, 500, 350 y 10.25. Así que completados los datos y ejecutado el análisis, veremos un gráfico que cubre una superficie y además presenta en su parte superior una referencia que dice 50%, 75%, 95% y 100%. Estos son los límites de confianza. Sin entrar en detalles estadísticos, estos límites nos dan idea de la probabilidad de acertar en el análisis, razón por la cual el gráfico correspondiente a un 50% es más estrecho que el de 75%, y éste que el de 95%. Es decir, con un menor porcentaje obtenemos una predicción más centrada y precisa, pero tenemos mayor riesgo de equivocarnos.
Más allá de la exactitud de las estimaciones, un análisis de sensibilidad, que podría también efectuarse simplemente cambiando varias veces el valor de un parámetro y observando lo que ocurre, nos muestra aquellas variables cuyos cambios afectan más el comportamiento del sistema, razón por la cual serán las que reciban mayor atención.
Interpretación de la gráfica
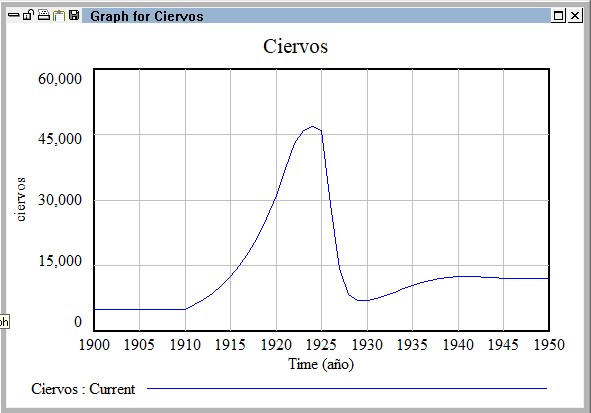
Veamos otro ejemplo representado por la gráfica siguiente, en la que podemos observar la evolución prevista desde 1900 a 1950 de la población de ciervos en una reserva natural.
A continuación simulamos la posibilidad de que el área de pastos de la reserva natural se vea reducida por causas naturales (incendios, desprendimientos de rocas, heladas, etc.) o por la gestión directa del parque (reserva de superficie para otras especies, etc.). Para ello hacemos una simulación de Montecarlo en la que el parámetro de superficie del parque podría llegar a ser la mitad de la superficie inicial. Los resultados se muestran en la gráfica siguiente.
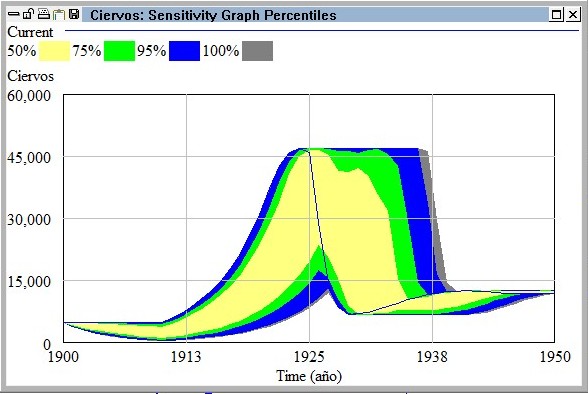En esta gráfica podemos ver la linea azul que muestra la simulación inicial y a su alrededor las zonas de color que muestran la distribución de probabilidad de la cantidad de ciervos en cada momento.
Así, vemos que hasta el año 1925 todos los escenarios están por debajo de la linea azul que muestra la simulación base, eso significa que cualquier disminución de la superficie de pasto se traducirá en mayor o menor medida en una disminución de la cantidad de ciervos. Este resultado era de esperar ya que si disminuye la superficie de pasto, disminuye el alimento disponible, y ello ha de provocar una disminución de la cantidad de ciervos.
Ahora bien, a partir en el periodo 1925-1935 se observa que lamayor parte de las distribuciones de probabilidad se hallan por encima de la línea del escenario base. La interpretación de esto que que durante ese periodo una posible disminución de la superficie de pasto se traducirá en una mayor cantidad de ciervos de la inicialmente prevista. Así por ejemplo en 1930 tenemos hasta un 50% de probabilidad de que la cifra de ciervos llegue a 40.000.
En el periodo 1940-1950 volvemos a observar una distribución de probabilidades similar a la anterior de 1925 en la que cualquier escenario de menos superficie de pasto se traduce en menor cantidad de ciervos.
Vemos pues como el Método de Montecarlo nos ofrece una visión menos determinista que la simulación normal de un modelo, ya que nos ofrece rangos de probabilidad del escenario base que estamos observando y una cuantificación del mismo. Si en 1930 el 50% de probabilidad sólo llegase a 10.000 ciervos podríamos decir que el escenario base es muy probable, pero teniendo en cuenta que la gráfica nos muestra que llega hasta los 40.000 ciervos podemos esperar con bastante seguridad que en 1930 tendremos bastantes más ciervos de los que hemos obtenido en el escenario base, ya que cualquier perturbación (a menos) de la superficie de pastos se traducirá en una mayor cantidad de ciervos.
<
