Ejercicio 5.22. El efecto mariposa
En el proceso de creación de un modelo de simulación es frecuente encontrar que los elementos del sistema se comportan de manera sorprendente e incluso totalmente inesperada. También puede ocurrir que los cambios que efectuamos en las condiciones iniciales produzcan efectos contrarios o muy distintos a los previstos, y aún más, que pequeños cambios en los valores iniciales generen grandes diferencias en el comportamiento de los elementos del sistema.
Quizás sin saberlo hemos creado un modelo de simulación con una estructura y una forma de relación entre variables tal que, bajo determinadas condiciones, presenta una forma de comportamiento que se conoce como caos. Una definición del caos establece que es "un comportamiento aperiódico en un sistema determinista que muestra gran sensibilidad respecto a las condiciones iniciales".
No es necesario que el modelo de simulación tenga un aspecto extremadamente complejo, con muchas variables, parámetros y retroalimentaciones. Los numerosos estudios realizados respecto al tema establecen que con tres ecuaciones diferenciales y una no-linealidad en alguna de ellas tenemos las condiciones necesarias para que el sistema presente bajo ciertas condiciones un comportamiento caótico.
En las últimas décadas del siglo XX la Teoría del Caos ha despertado considerable interés, ya que muestra la realidad interconectada que nos rodea y llena de bucles de retroalimentación, donde cada elemento integrante actúa para modificar el comportamiento del medio que la rodea, pero no lo hace en forma independiente sino obedeciendo a un comportamiento integrado del conjunto. Esta teoría es particularmente útil para abordar el estudio de los fenómenos sociales, siempre complejos y difíciles de resolver en términos de relaciones lineales causa-efecto.
Afortunadamente hay ejemplos de fenómenos físicos o de sistemas puramente matemáticos que facilitan la comprensión de los comportamientos caóticos antes de pasar a situaciones mucho más difíciles de modelar, como son los fenómenos sociales. Entre ellos, el péndulo forzado como fenómeno físico o una ecuación diferencial de tercer orden como modelo matemático. Tenemos otro ejemplo aún más conocido por sus repercusiones cinematográficas, originado en el trabajo del meteorólogo Edward Lorenz, quien hace más de cuarenta años construyó un sistema de tres ecuaciones diferenciales con el objeto de modelar de manera sencilla el comportamiento meteorológico, con el cual logró una respuesta tan sorprendente como llamativa y que se conoce popularmente como el "Efecto mariposa".
En la década de 1960 el meteorólogo Edward Lorenz inició una serie de investigaciones orientadas a resolver el problema de la predicción meteorológica. Trabajando sobre una atmósfera bidimensional rectangular, cuya zona inferior está a una temperatura mayor que la zona superior, y partiendo de las ecuaciones de continuidad, cantidad de movimiento y balance térmico, desarrolló un sistema simplificado formado por tres ecuaciones diferenciales.
Es importante observar que se trata de tres ecuaciones diferenciales que presentan dos no linealidades. Por ello este sistema reúne las condiciones para que aparezcan comportamientos caóticos en sus variables de estado (las "variables de estado" se denominan Niveles en Dinámica de Sistemas).
Podemos representar estas ecuaciones con un modelo de simulación dinámica. No obstante es necesario tener en cuenta que las ecuaciones precedentes resultan de un proceso usual en el análisis de fenómenos físicos y químicos, consistente en la adimensionalización de las variables. Consecuencia de este proceso es la aparición de agrupaciones de parámetros (por ejemplo densidad, viscosidad, longitudes características) conocidas como números adimensionales, que en definitiva establecen relaciones entre las fuerzas impulsoras del cambio en el sistema en estudio, o sea de su dinámica.
El modelo creado está formado de tres Niveles, denominados Flujo Convectivo, Diferencia de Temperatura Horizontal y Diferencia de Temperatura Vertical, que dependen de sus respectivos Flujos, que son: Variación del flujo convectivo, Variación de temperatura horizontal y Variación de temperatura vertical. Por otra parte, existen tres parámetros adimensionales: el Número de Prandtl, que establece una relación entre la viscosidad y la conductividad térmica del fluido, el Número de Rayleigh, que cuantifica la transmisión de calor en una capa de fluido con producción interna de calor por radiación, y la Altura, que representa el espesor de la capa en estudio.
En esencia, el modelo establece la relación entre el flujo convectivo y las variaciones de temperatura en la masa de aire, la cual es de por sí compleja dado que una diferencia de temperatura produce un flujo convectivo, pero a su vez este flujo modifica la diferencia de temperatura, todo ello condicionado a las propiedades del medio estudiado, tales como viscosidad, densidad, o conductividad térmica, las cuales se encuentran agrupadas en los números adimensionales que aparecen como parámetros del modelo.
Podemos construir un gráfico XY que nos compare la evolución conjunta de dos variables, por ejemplo el gráfico del Flujo Convectivo (en el eje X) en relación a la Diferencia de Temperatura Vertical (en el eje Y). Para hacerlo acudimos al menú de la barra superior: Windows - Control Panel - New y seleccionamos las variables tal y como se indica en la siguiente figura:
En rigor, lo que estamos haciendo es graficando el espacio de fases. El espacio de fases es el espacio matemático formado por las variables que describen un sistema dinámico. Cada punto del espacio de fases representa un posible estado del sistema. La evolución en el tiempo del sistema se representa con una trayectoria en el espacio de fases.
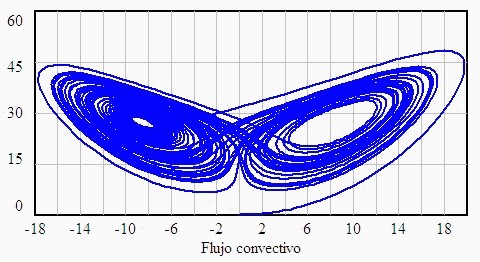
El estudio del espacio de fases reviste un interés especial. Los sistemas disipativos presentan regiones del espacio de fases hacia la cual convergen las trayectorias que parten de una determinada región, llamada "cuenca del atractor". Hay atractores predecibles, de estructura simple, como el punto o el ciclo límite. Pero hay otros atractores, conocidos como atractores extraños, en los cuales pequeñas diferencias en las posiciones iniciales conducen a posiciones que divergen totalmente. Este es precisamente el caso del atractor de Lorenz, con su curiosa forma similar a una mariposa.
Es probable que las evoluciones temporales de las variables, en general complejas, no permitan sacar conclusiones rápidas ni efectuar predicciones válidas, pero el análisis del espacio de fases si nos permite ver hacia donde converge el estado del sistema, y entre que valores máximos y mínimos de sus variables evoluciona. Todo esto constituye una información de gran valor cuando se aborda el estudio de las complejas situaciones que caracterizan al mundo en que vivimos.
Edward Lorenz descubrió este inesperado comportamiento en 1963, cuando efectuaba las primeras simulaciones con el modelo que estaba estudiando. Sin proponérselo, había desarrollado un valioso ejemplo práctico de comportamiento caótico, que venía a afirmar lo que ya se había planteado en forma teórica muchos años antes. En 1890 Henri Pointcaré publicó un artículo describiendo el hecho de que el sistema sol-tierra-luna no puede ser explicado bajo la mecánica tradicional. En sus palabras: "sucede que pequeñas diferencias en las condiciones iniciales impactan grandemente en el fenómeno final. Un pequeño cambio al principio provoca enormes errores al final. La predicción se vuelve imposible". Posteriores estudios acerca del tema han permitido desarrollar numerosos ejemplos de sistemas físicos, químicos, biológicos y matemáticos que presentan este fenómeno de impredecibilidad, el cual ha sido llamado "caos determinista".
Hallamos un buen ejemplo en el libro de Julien Sprott titulado "Chaos and Time-Series análisis" en el cual propone entre otros un sencillo modelo con tres variables. La visión sistémica y las poderosas herramientas de cálculo existentes permiten analizar muy rápidamente los problemas de comportamiento caótico, con la ventaja de disponer de una clara imagen visual de la estructura del sistema y sus interrelaciones. Asimismo, es inmediata la construcción de los espacios de fases y la búsqueda de atractores, lo cual no debe ser visto como un mero ejercicio matemático.
|
Información
