Ejercicio 5.18. Estudio de una catástrofe natural
 La Tierra de los Bosques es una región próspera situada en una región templada con abundante vegetación. Sus habitantes llevan una existencia feliz y placentera. En total son 1.000.000 de personas y esta cifra se ha mantenido estable en los últimos años.
Actualmente el 40% son jóvenes de menos de 20 años. Un 50% de la población es adulta, entre 20 y 70 años, y los otros son ancianos.
Por otra parte sabemos que sus parámetros poblaciones son los siguientes: su esperanza de vida es de 80 años, que la tasa de natalidad de la población adulta es del 6% anual, y que las tasas de mortalidad son el 2,5% para los jóvenes y del 2% para los adultos. Todos estos parámetros se han mantenido estables y no se espera que tengan modificaciones en el futuro.
Una noche desgraciada del verano del año 2005 se desata un terrible incendio, y durante una larga semana el fuego avanza sin control arrasando todo a su paso. Los servicios de emergencia consiguen poner a salvo a todos los jóvenes y los ancianos, pero cuando cesa el incendio descubren que el total de víctimas es de 100.000 personas siendo todas ellas adultas.
Se desea hacer una estimación de cual será la evolución del número de personas totales de la Tierra de los Bosques tras la catástrofe, sabiendo que los parámetros poblacionales (esperanza de vida, tasa de natalidad y tasas de mortalidad) van a permanecer constantes. Más concretamente se nos pide determinar el número de años que tardará la población en recuperar el valor de 1.000.000 de personas.
Para hacer este estudio vamos a hacer un sencillo modelo de simulación, de forma que se situaremos su fecha de inicio en el año 2000, y el horizonte temporal alcance 50 años.
Vamos a construir una primera versión del modelo en un escenario de población estable, del 2000 al 2050 recogiendo los parámetros que nos han facilitado. Después en una segunda versión introduciremos la muerte de 100.000 adultos en el año 2005 y evaluaremos su impacto hasta el año 2050.
Este modelo permite reproducir una situación estable. A continuación se modificará para simular la catástrofe. El primer efecto será sin duda una reducción de la población desde 1.000.000 a 900.000 personas, y queda por determinar la evolución futura. Sin duda la intuición del lector ya le indica cual va a ser ésta. Antes de seguir debería anotar el número de años aproximado que cree que tardará la población en volver a su cifra inicial de 1.000.000 personas.
Para simular los efectos de la catástrofe en el 2005 con un coste de 100.000 personas adultas, se crea un nuevo flujo de salida del nivel de adultos, y se utiliza la función PULSE, indicando que será en el periodo 2005 y tendrá una duración de 1 periodo.
Antes de simular podemos preguntarnos por el escenario que intuimos al cabo de 20 años, es decir:
a) la población permanecerá estable en 1.000.000 - 100.000 = 900.000
b) la población recuperará su valor inicial al cabo de pocos años
c) la población recuperará su valor inicial al cabo de muchos años.
Es importante antes de ejecutar un modelo permitir que nuestra intuición nos indique la evolución que esperamos observar en el modelo, ya que esto nos permite que cuando obtenemos los resultados estos confirmen nuestra intuición y por lo tanto tengamos una cierta base para en futuros estudios apoyarnos en ella, o bien los resultados contradigan nuestra intuición. En este último caso, si no hay ningún error en el modelo (cosa que deberemos verificar), es conveniente una reflexión que nos ayude a reconsiderar los supuestos en los que hemos basado nuestra intuición.
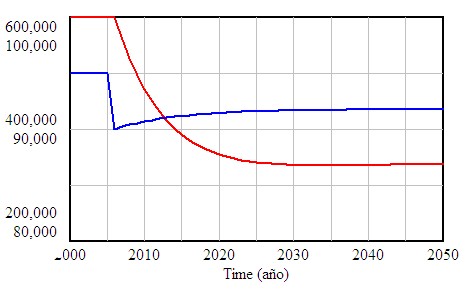
El modelo nos muestra con claridad una evolución del número total de personas que no coincide con nuestras expectativas ya que ni la población se mantiene en la cifra de 900.000 personas ni se recupera la cifra del total de la población en el amplio horizonte que hemos tomado, sino que se estabiliza en un valor claramente inferior a las 900.000 personas.
Podemos hacer un seguimiento de lo que sucede en los diversos colectivos a través de las gráficas que nos muestran la evolución de una variable y de aquellas que la influyen.
La Tierra de los Bosques es una región próspera situada en una región templada con abundante vegetación. Sus habitantes llevan una existencia feliz y placentera. En total son 1.000.000 de personas y esta cifra se ha mantenido estable en los últimos años.
Actualmente el 40% son jóvenes de menos de 20 años. Un 50% de la población es adulta, entre 20 y 70 años, y los otros son ancianos.
Por otra parte sabemos que sus parámetros poblaciones son los siguientes: su esperanza de vida es de 80 años, que la tasa de natalidad de la población adulta es del 6% anual, y que las tasas de mortalidad son el 2,5% para los jóvenes y del 2% para los adultos. Todos estos parámetros se han mantenido estables y no se espera que tengan modificaciones en el futuro.
Una noche desgraciada del verano del año 2005 se desata un terrible incendio, y durante una larga semana el fuego avanza sin control arrasando todo a su paso. Los servicios de emergencia consiguen poner a salvo a todos los jóvenes y los ancianos, pero cuando cesa el incendio descubren que el total de víctimas es de 100.000 personas siendo todas ellas adultas.
Se desea hacer una estimación de cual será la evolución del número de personas totales de la Tierra de los Bosques tras la catástrofe, sabiendo que los parámetros poblacionales (esperanza de vida, tasa de natalidad y tasas de mortalidad) van a permanecer constantes. Más concretamente se nos pide determinar el número de años que tardará la población en recuperar el valor de 1.000.000 de personas.
Para hacer este estudio vamos a hacer un sencillo modelo de simulación, de forma que se situaremos su fecha de inicio en el año 2000, y el horizonte temporal alcance 50 años.
Vamos a construir una primera versión del modelo en un escenario de población estable, del 2000 al 2050 recogiendo los parámetros que nos han facilitado. Después en una segunda versión introduciremos la muerte de 100.000 adultos en el año 2005 y evaluaremos su impacto hasta el año 2050.
Este modelo permite reproducir una situación estable. A continuación se modificará para simular la catástrofe. El primer efecto será sin duda una reducción de la población desde 1.000.000 a 900.000 personas, y queda por determinar la evolución futura. Sin duda la intuición del lector ya le indica cual va a ser ésta. Antes de seguir debería anotar el número de años aproximado que cree que tardará la población en volver a su cifra inicial de 1.000.000 personas.
Para simular los efectos de la catástrofe en el 2005 con un coste de 100.000 personas adultas, se crea un nuevo flujo de salida del nivel de adultos, y se utiliza la función PULSE, indicando que será en el periodo 2005 y tendrá una duración de 1 periodo.
Antes de simular podemos preguntarnos por el escenario que intuimos al cabo de 20 años, es decir:
a) la población permanecerá estable en 1.000.000 - 100.000 = 900.000
b) la población recuperará su valor inicial al cabo de pocos años
c) la población recuperará su valor inicial al cabo de muchos años.
Es importante antes de ejecutar un modelo permitir que nuestra intuición nos indique la evolución que esperamos observar en el modelo, ya que esto nos permite que cuando obtenemos los resultados estos confirmen nuestra intuición y por lo tanto tengamos una cierta base para en futuros estudios apoyarnos en ella, o bien los resultados contradigan nuestra intuición. En este último caso, si no hay ningún error en el modelo (cosa que deberemos verificar), es conveniente una reflexión que nos ayude a reconsiderar los supuestos en los que hemos basado nuestra intuición.
El modelo nos muestra con claridad una evolución del número total de personas que no coincide con nuestras expectativas ya que ni la población se mantiene en la cifra de 900.000 personas ni se recupera la cifra del total de la población en el amplio horizonte que hemos tomado, sino que se estabiliza en un valor claramente inferior a las 900.000 personas.
Podemos hacer un seguimiento de lo que sucede en los diversos colectivos a través de las gráficas que nos muestran la evolución de una variable y de aquellas que la influyen.
|

 Información
Información




 Información
Información


