Abstract

Se presentan varios modelos de sistemas físicos desarrollados con dinámica de sistemas: estos han sido usados en un curso de Física General en la Universidad de Costa Rica. Los modelos han demostrado ser una herramienta valiosa en la comprensión de los conceptos físicos, y a la vez poseen la ventaja de ser relativamente sencillos para el uso de los estudiantes.

Introducción

La dinámica de sistemas (DS) se ha usado en el modelado de sistemas sociales, económicos, biológicos, químicos, físicos, etc. En particular, en varios lugares la dinámica de sistemas se ha utilizado para la enseñanza de la física. Los conceptos básicos de stock, flujos, conectores y variables auxiliares permiten que los estudiantes expuestos a la DS empiecen a desarrollar modelos básicos muy rápidamente. De hecho, la DS se está usando con estudiantes de escuela primaria y secundaria en varios países, y en varias disciplinas (incluyendo literatura e historia). El grado de éxito de estos proyectos ha sido variable, pero se cuenta con buenas experiencias, y se puede afirmar que los estudiantes asimilan bastante bien los conceptos básicos de la DS.

La DS se utilizó como parte del laboratorio que acompaña al curso Física General 1 que se enseña en la Universidad de Costa Rica, para estudiantes de las diferentes carreras de ingeniería. Este laboratorio tiene una duración de 3 horas, y se imparte una vez a la semana. Los estudiantes no tenían ningún conocimiento previo de DS. Hasta donde el autor conoce, esta es la primera vez que se usa la DS en el ámbito de la enseñanza de la física en Costa Rica.

Materiales y métodos

La DS se utilizó a lo largo del año 2023 con dos grupos de laboratorio de física general. Este curso explora durante el semestre (de 17 semanas de duración) los conceptos básicos de la mecánica clásica y el trabajo de laboratorio en física. El laboratorio es el complemento práctico del curso de teoría, el cual los estudiantes deben llevar junto con el laboratorio. Uno de los grupos de laboratorio se dio durante el primer semestre (marzo a julio), mientras que el segundo grupo se enseñó en el segundo semestre del año (agosto a diciembre). El tamaño de ambos grupos fue el mismo: 20 estudiantes por grupo, 2 estudiantes por mesa.
Los estudiantes no tenían ningún conocimiento previo de DS, por lo que la primera mitad del semestre se usó para que los estudiantes adquirieran los conceptos básicos utilizando el software de modelado Insight Maker.
Las explicaciones iniciales giraron alrededor del vocabulario de la DS: stocks, flujos, conectores causales, y variables auxiliares. A este efecto se desarrollaron modelos muy sencillos de sistemas dinámicos: la dinámica de una cuenta de ahorros y el crecimiento de una población.
Una vez que los estudiantes manejaban las herramientas básicas, se introdujo el siguiente paradigma de simulación de sistemas mecánicos de física clásica:

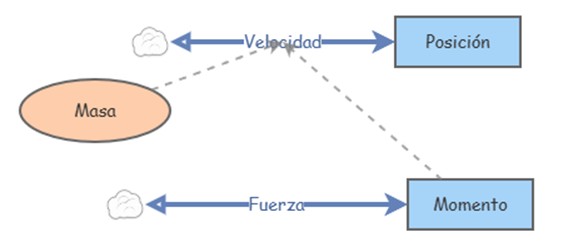
Figura 1. Modelo base para las simulaciones.

Este modelo base permite usar la segunda ley de Newton para describir el movimiento de una masa puntual sometida a la acción dinámica de una fuerza cualquiera (la fuerza puede ser constante, función del tiempo, o de la posición, etc.). El cambio en el momento se asocia con la fuerza aplicada, y hace que la velocidad de la masa cambie. De manera simultánea, el flujo representado por la velocidad hace que la posición de la partícula varíe en el tiempo.
Las ecuaciones diferenciales involucradas en este sistema son:
F = dp/dt / v = dx/dt
donde F: fuerza aplicada, p: momentum lineal, x: posición, t: tiempo

Desde el punto de vista conceptual, los estudiantes pueden percibir la relación causal entre el flujo Fuerza y el stock Momento. La cantidad de movimiento lineal cambia únicamente por la acción de una fuerza aplicada, mientras que existe una relación causal entre el momento y la velocidad (pero no un flujo). Al correr el modelo para diferentes valores de la masa, los estudiantes deben reflexionar sobre el significado de los conceptos de los elementos del modelo, y su relación con las variables físicas del mismo. Esta reflexión es, a veces, difícil de lograr para los estudiantes en el curso de teoría, en el cual se pasa muy rápido sobre los temas.

Una de las ventajas de este tipo de modelos es que permite contestar de manera muy sencilla preguntas del tipo “¿qué pasaría …. si?. Los estudiantes pueden visualizar que variando la “entrada” al stock momento, es decir cambiando la fuerza, varía la cinemática del sistema, y que este cambio se verá reflejado en un cambio en la posición, velocidad y aceleración del objeto sobre el cual se aplica la fuerza.

Se desarrollaron varios modelos, además del modelo base mostrado arriba. En el modelo base se consideró el caso de una fuerza constante. En los siguientes modelos las fuerzas consideradas fueron:
F = t: donde t es el tiempo en segundos. Aquí se utilizó la función Seconds() que Insight Maker tiene en su librería de funciones.
F = sen(t): una función trigonométrica.
F = 1.0 * x: donde x es la posición instantánea de la masa.
Las figuras siguientes presentan algunos de los resultados:

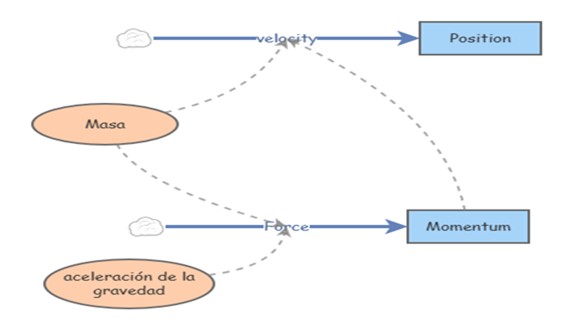
Figura 2. Movimiento de una masa puntual bajo la influencia de la gravedad terrestre.

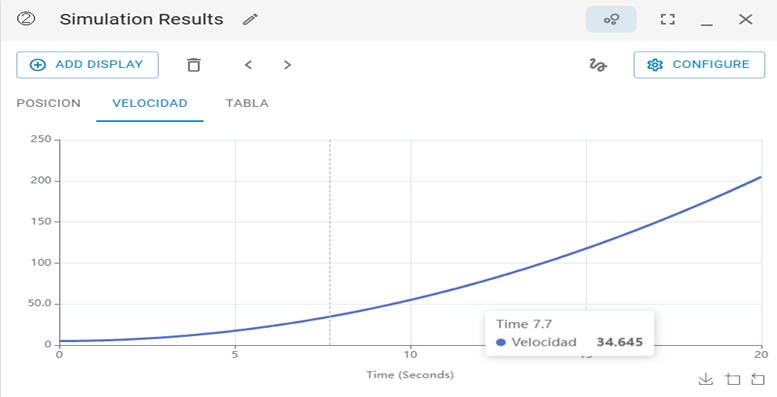
Figura 3. Velocidad en función del tiempo para una masa sujeta a una fuerza del tipo F= t.

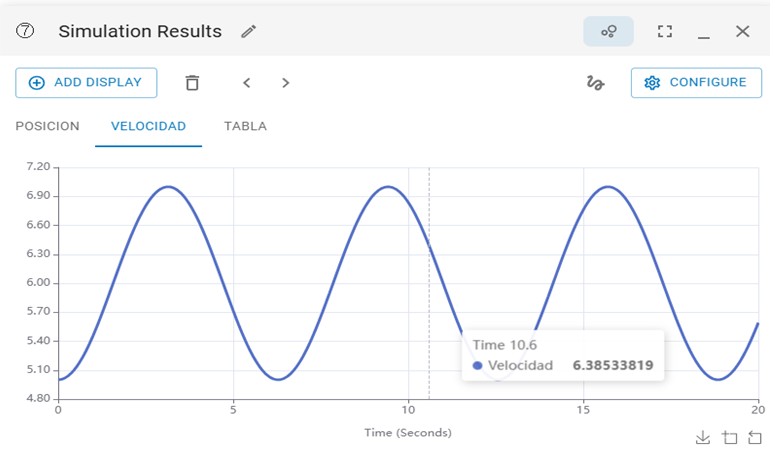
Figura 4. Velocidad en función del tiempo para una masa sujeta a una fuerza F = sen(t).

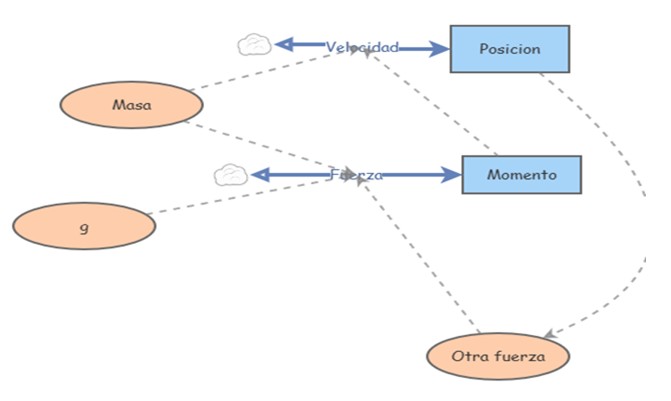
Figura 5. Modelo para simular fuerzas que dependen de la posición de la partícula.

Conclusiones

1. La enseñanza de los conceptos cinemáticos de la mecánica clásica se puede facilitar con el uso de la dinámica de sistemas, la cual permite ver los cambios en los stocks (acumulaciones) como resultado de los flujos hacia y desde los mismos stocks.
2. En mecánica clásica el fuljo que cambia la cantidad de movimiento lineal de un sistema de partículas es la fuerza aplicada sobre el sistema. Con Insight Maker, es posible ver gráficamente (y de manera instantánea) el efecto que la fuerza ejercida tiene sobre la posición, la velocidad y la aceleración de las masas puntuales.
3. Los conceptos básicos de la dinámica de sistemas son asimilados rápidamente por los estudiantes, lo cual permite que estos estén en capacidad de modelar sistemas sencillos en un tiempo relativamente breve.
4. Insight Maker tiene una librería de funciones muy grande, lo cual permite que los estudiantes utilicen fuerzas de tipos muy diversos para explorar la respuesta dinámica de la masa ante diferentes inputs.
5. Los estudiantes pueden relacionar el uso de los modelos de DS con el curso de ecuaciones diferenciales, ya que Insight Maker resuelve de manera numérica las relaciones entre variables cinemáticas (estas relaciones se expresan como ecuaciones que relacionan las variables con sus diferentes derivadas respecto al tiempo).
6. Es posible, y de manera muy sencilla, extender estos modelos para incluir temas como movimiento en medios resistivos (como el aire), movimiento de proyectiles, y conservación de la energía mecánica. También se pueden explorar temas como electromagnetismo y termodinámica.
7. Los estudiantes obtienen una visión más conceptual de la primera y segunda leyes de Newton, al tener que relacionar el concepto de fuerza con el concepto de flujo. A la vez, la DS les permite obtener respuestas numéricas a problemas de cálculo diferencia e integral; estas respuestas pueden ser verificadas de manera manual, lo cual ayuda directamente a los estudiantes a cimentar los conceptos matemáticos.

(*) Puede solicitar información más detallada de este trabajo a los autores

---