|
El modelo de difusión de Bass es un modelo matemático utilizado para describir cómo los productos nuevos o las innovaciones se adoptan dentro de un mercado o una población a lo largo del tiempo. Fue desarrollado por Frank M. Bass en 1969 y se utiliza ampliamente en marketing, economía y gestión para predecir la adopción de productos y tecnologías, como teléfonos inteligentes, electrodomésticos o servicios de software.
Componentes clave del modelo
El modelo asume que la adopción de un producto está impulsada por dos factores principales:
1. Innovadores (coeficiente de innovación, \(p\))**: Son los primeros adoptantes que adoptan el producto por iniciativa propia, sin influencia de otros. Representan una proporción de consumidores motivados por la novedad del producto o la innovación tecnológica.
2. Imitadores (coeficiente de imitación, \(q\))**: Son los consumidores que adoptan el producto debido a la influencia social o el boca a boca, es decir, la interacción con otros usuarios que ya lo han adoptado.
Suposiciones del modelo
1. Toda la población potencial de adoptantes está fija y conocida de antemano.
2. Los consumidores solo adoptan el producto una vez.
3. No se tienen en cuenta factores externos como cambios en precios, calidad o marketing adicional.
Curva de adopción
El modelo de Bass produce una curva característica con forma de "S", que consta de tres fases:
1. Introducción: La adopción es lenta debido a la influencia inicial de los innovadores.
2. Crecimiento acelerado: La adopción crece rápidamente a medida que los imitadores comienzan a adoptar el producto.
3. Madurez: El crecimiento disminuye cuando el mercado se aproxima a la saturación.
Aplicaciones
- Predicción de ventas: Estimar la demanda futura de un producto nuevo.
- Estrategias de marketing: Identificar el momento óptimo para campañas publicitarias.
- Planificación de capacidad: Prever la demanda para ajustar la producción o la distribución.
El modelo de Bass es particularmente útil para productos con ciclos de vida bien definidos y se puede ajustar o extender para considerar variaciones en precios, competencia y otras dinámicas del mercado.
A continuación se muestra un modelo de simulación en el que se ha tomado como base un Modelo de Bass básico, y se lo ha extendido en otros aspectos.
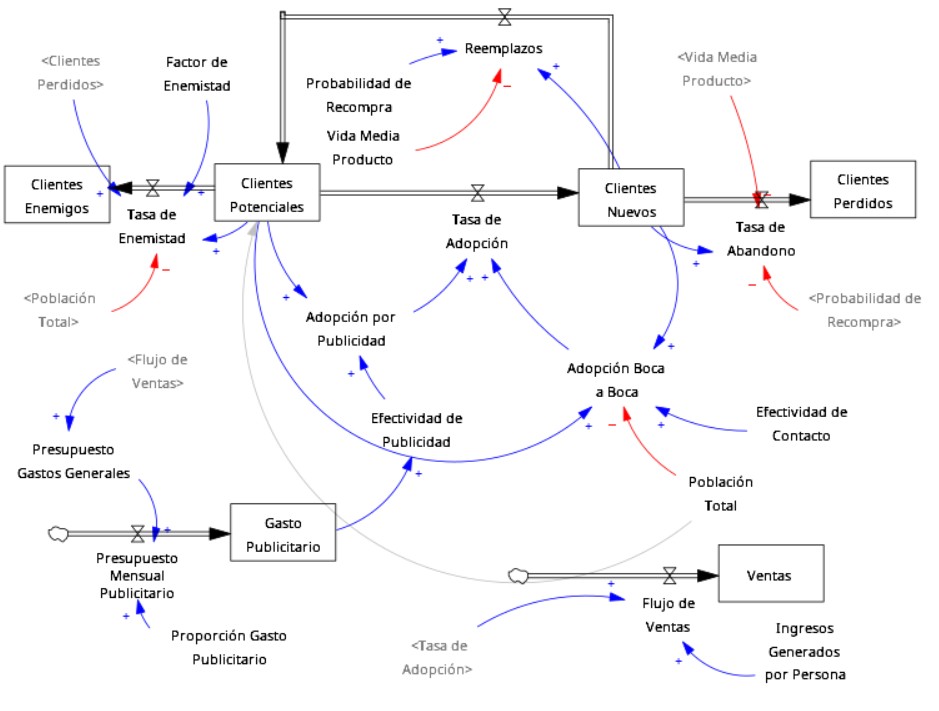
Proceso de Recompra y de Pérdida Definitiva de Clientes: La intención es mostrar cómo los "clientes nuevos" (es decir, clientes que compraron el producto) deciden recomprar o no el producto una vez que la vida del mismo ha llegado a su fin (por el motivo que sea, rotura, desgaste natural, pérdida, etc.). La "vida media" se simula con una función RANDOM EXPONENCIAL para poder capturar la naturaleza asimétrica y decreciente de la duración de los productos en el mercado (en la mayoría de los casos los productos tienen una duración más corta, aunque existen casos poco frecuentes donde los productos logran tener una vida útil más larga).
Proceso de Enemistad: Así como existe un "boca a boca" positivo, también existe uno negativo (creo honestamente que en la realidad un cliente insatisfecho y enemigo de una marca genera un impacto sustancialmente mayor que uno realmente satisfecho). El objetivo fue modelar cómo un porcentaje de "clientes perdidos" (clientes que deciden no recomprar el producto) inciden negativamente sobre la base de "clientes potenciales", haciendo que muchos de estos clientes potenciales se transformen en "enemigos" de la marca sin siquiera haber llegado a probar el producto. La variable "factor de enemistad" se simula con una función aleatoria normal.
Proceso de Ventas: Esta sección del modelo le permite al usuario ver el flujo mensual de ventas y la venta acumulada. Además, se introduce la posibilidad de que en cada compra la persona pueda comprar más de un producto (se simula que la persona puede comprar entre 1 y 6 productos mediante una función RANDOM EXPONENTIAL).
Gasto Publicitario: El haber obtenido el flujo de ventas en cada periodo, y al haber supuesto una estructura de costos donde el 20% del dinero que ingresa se destina a cubrir los gastos generales de la empresa, se simula aquí que un 5% de ese 20% se destina a campañas publicitarias. Aquí introduje la innovación de que el "gasto publicitario" acumulado puede determinar la "efectividad de la publicidad" (en todos los modelos de Bass que conozco siempre se considera este valor como constante, y considero que no lo debe ser). En este sentido, se determina que la "efectividad de la publicidad" sigue la lógica de una función logarítmica, es decir, tiene rendimientos decrecientes (mayores inversiones publicitarias generan un impacto cada vez menor en la efectividad). Se introduce un factor "k" que nos permite ajustar la fórmula para que la efectividad de la publicidad permanezca en un rango razonable, alineado con otras variables del modelo.
Si bien al modelo se lo podría enriquecer con otras variables (como la posibilidad de competidores/productos sustitutos, la creación de nuevos modelos que reemplacen al producto actual (estilo Samsung S23 vs Samsung S24, potenciales crisis económicas, etc.), considero que el mismo es bastante bueno para enseñar conceptos básicos de dinámica de sistemas y negocios.
Resultados
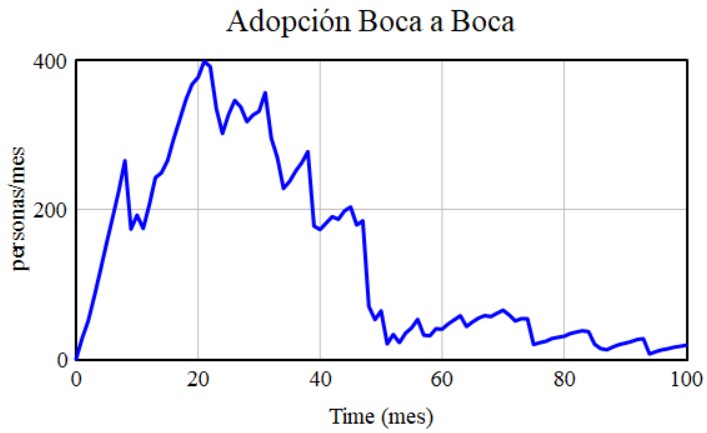
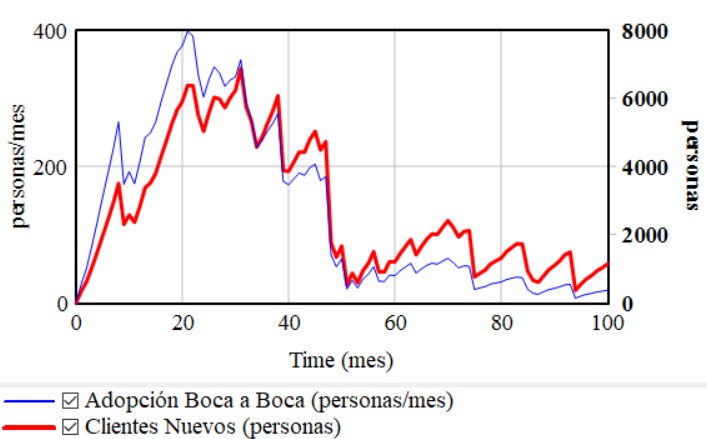
(*) Si lo desea puede solicitar información más detallada de este trabajo al autor del texto
|