Dinámica del crecimiento poblacional de un centro urbano
Basado en un modelo de simulación con Vensim
Juan Pablo Londoño Linares
jplondo@yahoo.com
El problema que se presenta tiene que ver con los patrones de urbanización de una ciudad. Específicamente se trata de modelar la dinámica del crecimiento poblacional de un centro urbano en función de su área disponible para expansión.
Inicialmente, se tiene un área total de 550 Km2, de la cual, según los lineamientos establecidos por el municipio, existen solo 165 Km2 donde se puede construir, quedando los restantes 385 como zona protegida (por su ecosistema, y sus condiciones difíciles como altas pendientes y cercanía a márgenes de ríos). En el área donde es posible construir se tendrá que un 50% debe corresponder a espacio público (parques, vías, plazas, etc.), quedando el otro 50% como área efectiva de viviendas.
La población inicial del municipio son 380.000 habitantes.
Se supondrá que una familia promedio de cinco personas vive en una casa que ocupa 100 m2, por consiguiente, cada persona requerirá de un área para vivir de 20 m2/hab.
En un primer escenario se tiene una población estática, con tasas de inmigración y emigración iguales y constantes. Se observa del modelo Version1, que el déficit de vivienda (ya negativo en sus inicios) se va reduciendo con el tiempo. Esto es natural, pues se ha supuesto un aumento de urbanización a una tasa constante anual, manteniendo una población constante que requiere un área menor a la disponible. El modelo permite establecer la tasa de urbanización en metros cuadrados contruidos por año, necesaria para que se sature el área urbanizable y permite estimar el número de años necesarios para que se dé este proceso. Por otro lado, aumentando la tasa de inmigración, permitirá saber cuántos años podrá seguir asimilando población el municipio, hasta que el déficit de vivienda comience a tomar valores positivos.
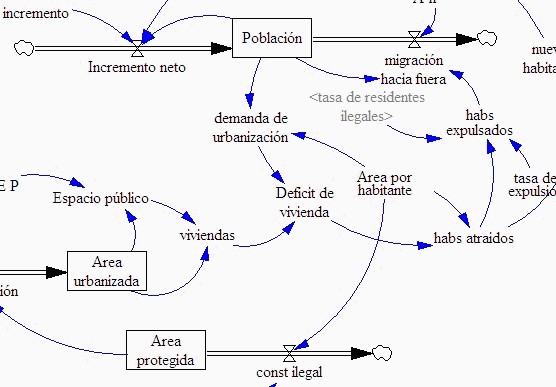
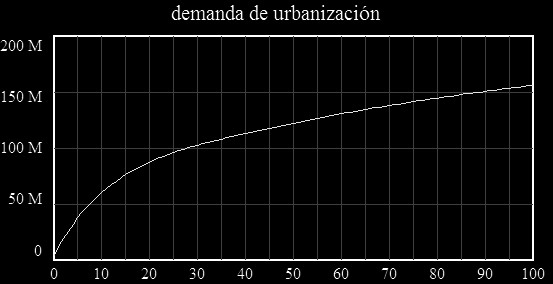
En una Version 2 del modelo se tiene en cuenta la capacidad de soporte de la ciudad, es decir, la población que efectivamente podría vivir allí. A partir de la curva de esta variable puede deducirse cuántos años, siguiendo con las políticas establecidas, puede seguir creciendo la ciudad sin presentar problemas de espacio, y cuánto tiempo puede seguir aceptando más población de fuera.
En la Version 3 se tiene en cuenta la asimilación o expulsión de la población atraída. Inicialmente se supone que la población atraída va a formar parte de la población residente como nuevos habitantes, en la medida en que haya espacio suficiente para habitar. En el caso contrario constituirían la población expulsada, y saldrían hacia otros sitios por emigración, regulando así la población total según la capacidad del municipio.
La Versión 4 adiciona al modelo la siguiente consideración: cuando hay un exceso de habitantes, una parte de ellos se convierte en residentes ilegales (tasa de residentes ilegales, que es el % de los habitantes en exceso que se quedarían como residentes ilegales, siendo los demás expulsados. Se ha supuesto que estos residentes ilegales construyen sobre las áreas protegidas de manera ilegal. De esta manera, es posible modificar tasas de aceptación de población, los valores de expulsados, las tasas de crecimiento, etc., y ver que sucede. Básicamente se observa que cuando el municipio está creciendo y hay mucha área disponible para urbanización, la población crece, hasta llegar a un punto en el cual empieza a presentarse exceso de población, y con ello expulsión de la misma y construcción ilegal, con la consecuente reducción de las áreas protegidas.
Según Wikipedia la dinámica de sistemas es una técnica para analizar y modelar el comportamiento temporal en entornos complejos. Se basa en la identificación de los bucles de realimentación entre los elementos, y también en las demoras en la información y materiales dentro del sistema. Lo que hace diferente este enfoque de otros usados para estudiar sistemas complejos es el análisis de los efectos de los bucles o ciclos de realimentación, en términos de flujos y depósitos adyacentes. De esta manera se puede estructurar a través de modelos matemáticos la dinámica del comportamiento de estos sistemas. La simulación de estos modelos actualmente se puede realizar con ayuda de programas computacionales específicos.
Originalmente desarrollada en 1950 para ayudar a los administradores de empresas a mejorar su comprensión de los procesos industriales, actualmente se usa en el sector público y privado para el análisis y diseño de políticas. Fue creada a principios en la década de 1960 por Jay Forrester de la MIT Sloan School of Management del Massachusetts Institute of Technology) con la creación del MIT System Dynamics Group.
Los modelos de simulación con Dinámica de Sistemas tienen aplicaciones en prácticamente todas las áreas del conocimiento como podemos observar en los numerosos artículos publicados en los congresos anuales de la System Dynamics Society. Se trata de una potente herramienta para:
Enseñar a los reflejos del sistema de pensamiento de las personas que está siendo entrenado.
Analizar y comparar los supuestos y modelos mentales acerca de cómo funcionan las cosas.
Obtener una visión cualitativa sobre el funcionamiento de un sistema o las consecuencias de una decisión.
Reconocer arquetipos de sistemas disfuncionales en la práctica diaria.
Los modelos permiten simular el impacto de diferentes políticas relativas a la situación a estudiar ejecutando simulaciones what if (¿qué pasaría si?) que permiten ver las consecuencias a corto y medio plazo, y ser de gran ayuda en la comprensión de cómo los cambios en un sistema lo afectan en el tiempo. En este sentido es muy similar al Pensamiento sistémico ya que se basa en los mismos diagramas de causales con bucles o lazos de retroalimentación (feedback). Sin embargo, estos modelos de simulación permiten además hacer simulaciones para estudiar el comportamiento de los sistemas y el impacto de políticas alternativas. Se utiliza en especial para investigar la dependencia de los recursos naturales y los problemas resultantes del creciente consumo a nivel global para mejorar el especial en el desarrollo de nuevos productos. Existe una gran variedad de marcas de software en el mercado que ayudan a aplicar esta herramienta de una forma amigable: Vensim, Stella, ithink, Powersim, Dynamo, etc.
(*) Puede solicitar información más detallada de este trabajo al autor
|





