El atractor mariposa o atractor de Lorenz
Basado en un modelo de simulación con Vensim
Claudio M. Enrique
cenrique@fiqus.unl.edu.ar; cenriquear@yahoo.com.ar
Hace un tiempo escribí un artículo en este Boletín relacionado con la Teoría del Caos, los Sistemas Oscilatorios y la Dinámica de Sistemas, donde hacía hincapié en la utilidad que presenta ésta última como herramienta para introducir el estudio de la mencionada Teoría en cursos universitarios de grado y, por que no, en niveles de secundario.
En este trabajo se presenta un "pasito" más en el empleo de la DS para el estudio del Caos, donde se realiza un análisis particular de un atractor de los más conocidos: el atractor mariposa o de Lorenz.
Antes, vamos a recordar que un atractor es una singularidad en el espacio de acción donde ocurre un fenómeno, hacia el cual convergen las trayectorias de una dada dinámica, que encuentran en su atractor una condición local de mínima energía. La existencia de un atractor se puede detectar observando la disipación de algún tipo de energía. El atractor de un péndulo oscilando libremente es su punto más bajo, y es puntual. Además de atractores puntuales, existen atractores cíclicos - o ciclos límites - y atractores caóticos o atractores extraños - el conjunto límite de una trayectoria caótica -.
El concepto opuesto es un repulsor, que está asociado con la inestabilidad de una esfera ubicada en el pico de una montaña.
El comportamiento del modelo de Lorenz se puede representar trazando sus variables en el espacio de fase. Es decir que para cada cálculo sucesivo de x, y, y z, se traza el punto correspondiente en un espacio de ejes xyz. En un sistema lineal este trazado puede dibujar una trayectoria conducente a un único punto de estabilidad, o alternativamente puede dibujar un bucle cerrado que indica una variación periódica.
El atractor de Lorenz es uno de los que pertenecen a un conjunto denominado como atractores desconocidos. Si bien no es una estructura geométrica sencilla, tampoco resulta ser una curva complicada. Se caracteriza porque nunca se intersecta a sí mismo ni repite la misma trayectoria. Proyectado en el plano xz, el atractor se parece a una mariposa; mientras que en el plano yz, se asemeja a una máscara de lechuza. La proyección en el palno xy resulta útil para percibir la tridimensionalidad de este atractor.
Puntualmente, para estudiar este atractor, he empleado las siguientes ecuaciones :
dx/dt = -s x + s y
dy/dt = -x y + r x - y
dz/dt = x y - b z
donde s; b; y r son tres constantes que determinan el comportamiento del sistema.
Para el modelo empleado, se usaron los valores siguientes para las constantes:
s =10;
b = 8 / 3;
r = 28
El modelo de Dinámica de Sistemas que he creado para estudiar al atractor mariposa es el siguiente:
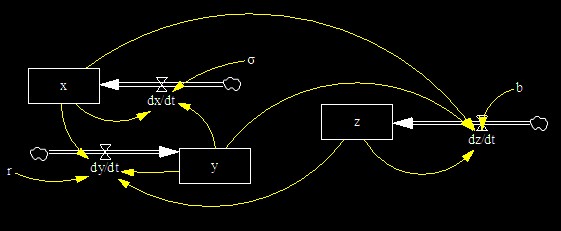
que me ha permitido obtener estas representaciones gráficas:
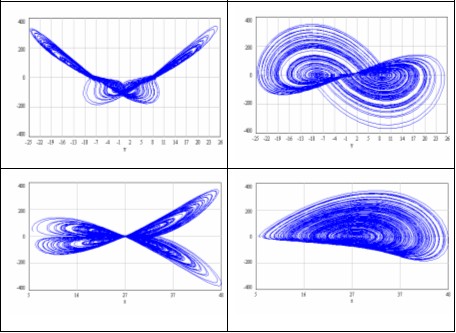
Si bien este artículo es de carácter introductorio, resulta evidente que el uso de la Dinámica de Sistemas puede favorecer enormemente el proceso de enseñanza - aprendizaje sobre la Teoría del Caos, y sin tantas complicaciones vinculadas con la Matemática. Espero que este artículo contribuya para tales fines educativos.
Según Wikipedia la dinámica de sistemas es una técnica para analizar y modelar el comportamiento temporal en entornos complejos. Se basa en la identificación de los bucles de realimentación entre los elementos, y también en las demoras en la información y materiales dentro del sistema. Lo que hace diferente este enfoque de otros usados para estudiar sistemas complejos es el análisis de los efectos de los bucles o ciclos de realimentación, en términos de flujos y depósitos adyacentes. De esta manera se puede estructurar a través de modelos matemáticos la dinámica del comportamiento de estos sistemas. La simulación de estos modelos actualmente se puede realizar con ayuda de programas computacionales específicos.
Originalmente desarrollada en 1950 para ayudar a los administradores de empresas a mejorar su comprensión de los procesos industriales, actualmente se usa en el sector público y privado para el análisis y diseño de políticas. Fue creada a principios en la década de 1960 por Jay Forrester de la MIT Sloan School of Management del Massachusetts Institute of Technology) con la creación del MIT System Dynamics Group.
Los modelos de simulación con Dinámica de Sistemas tienen aplicaciones en prácticamente todas las áreas del conocimiento como podemos observar en los numerosos artículos publicados en los congresos anuales de la System Dynamics Society. Se trata de una potente herramienta para:
Enseñar a los reflejos del sistema de pensamiento de las personas que está siendo entrenado.
Analizar y comparar los supuestos y modelos mentales acerca de cómo funcionan las cosas.
Obtener una visión cualitativa sobre el funcionamiento de un sistema o las consecuencias de una decisión.
Reconocer arquetipos de sistemas disfuncionales en la práctica diaria.
Los modelos permiten simular el impacto de diferentes políticas relativas a la situación a estudiar ejecutando simulaciones what if (¿qué pasaría si?) que permiten ver las consecuencias a corto y medio plazo, y ser de gran ayuda en la comprensión de cómo los cambios en un sistema lo afectan en el tiempo. En este sentido es muy similar al Pensamiento sistémico ya que se basa en los mismos diagramas de causales con bucles o lazos de retroalimentación (feedback). Sin embargo, estos modelos de simulación permiten además hacer simulaciones para estudiar el comportamiento de los sistemas y el impacto de políticas alternativas. Se utiliza en especial para investigar la dependencia de los recursos naturales y los problemas resultantes del creciente consumo a nivel global para mejorar el especial en el desarrollo de nuevos productos. Existe una gran variedad de marcas de software en el mercado que ayudan a aplicar esta herramienta de una forma amigable: Vensim, Stella, ithink, Powersim, Dynamo, etc.
(*) Puede solicitar información más detallada de este trabajo al autor
|





