Modelo de los Movimientos Oscilatorios y la Teoría del Caos

Basado en un modelo de simulación con Vensim

Claudio M. Enrique
cenrique@fiqus.unl.edu.ar; cenriquear@yahoo.com.ar

Hace unas semanas llegó a mis manos un ejemplar titulado "La esencia del caos", de Edward Lorenz. Este autor es un meteorólogo muy conocido, y, como para presentarlo "en sociedad", escribió en 1972 un artículo titulado "Predecibilidad. El aleteo de una mariposa en Brasil, originó un tornado en Texas?". Como se deduce fácilmente, es lo que conocemos como "efecto mariposa", si bien Lorenz normalmente con esta oración se ha referido al primer sistema caótico que ha estudiado en detalle.

En este libro sobre Teoría del Caos he encontrado que se menciona mucho, como ejemplo sencillo y de fin introductor, al péndulo de un reloj. Además, como docente universitario de Física, siempre me ha interesado la gestión del proceso de enseñanza - aprendizaje con conceptos actuales: no olvidemos que estamos en el Siglo XXI, y que los problemas nuevos nunca se han resuelto con recetas antiguas. Pues bien, me ha parecido una idea interesante poder usar el modelo de los movimientos oscilatorios en esta "introducción" sobre el caos, pero cambiando el tipo de péndulo a usar- el de resorte es el que ha sido presentado en ediciones anteriores del BADS -.

El modelo que se usa en este artículo es el de un péndulo simple forzado; es decir que se trata de un sistema oscilante constituido por una masa puntual, sostenida por un hilo de longitud l y de masa despreciable, donde actúa una fuerza exterior periódica del tipo F(t) = F . cos (wt ), junto a una fuerza de rozamiento proporcional a la velocidad FRoz = - b . vx , y es el que se presenta a continuación:

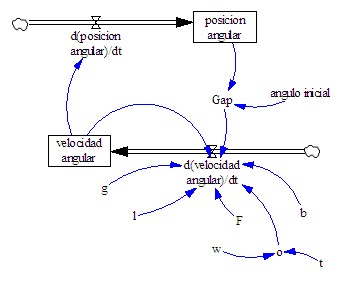
Si bien se pueden trabajar tanto con variables angulares como lineales para describir el movimiento de este péndulo, he optado por la primer alternativa por ser una situación más acorde a la realidad.

Respecto a la Teoría del Caos, muchas veces se menciona a un atractor. Atractor es una singularidad en el espacio de fase donde ocurre un fenómeno, hacia el cual convergen las trayectorias de una dada dinámica que encuentran - en dicho atractor - una condición local de mínima energía. La existencia de un atractor se puede detectar observando la disipación de algún tipo de energía. El atractor (puntual) de un péndulo oscilando libremente es su punto más bajo. Además de atractores puntuales, hay atractores cíclicos (o ciclos límites) y atractores caóticos o atractores extraños (el conjunto límite de una trayectoria caótica).

Con este modelo, podemos ver si existe o no un atractor. Partiendo de un sistema amortiguado - dándole en el modelo a F(t) el valor de cero - , podemos analizar un péndulo que tiene existencia real debido a que la mayoría de los péndulos simples analizados un tiempo relativamente largo experimentan una disminución de su amplitud debido al rozamiento. Para nuestro estudio, es un sistema disipativo: un sistema dinámico en el que la imagen de cualquier conjunto de puntos de volumen infinito en el espacio de fase es un conjunto de menor volumen. Ahora, veamos que dice Lorenz al respecto: "Un atractor puede ser a veces un punto único. Un péndulo de un reloj al que no se dé cuerda llegará a detenerse, colgando verticalmente, sin importar cómo se lo haya puesto inicialmente en movimiento. Como el estado del péndulo, antes de llegar al reposo, puede describirse mediante dos variables, el espacio de fase del péndulo debe ser bidimensional; debe ser un plano. En este plano podemos elegir una distancia horizontal a un punto desde el origen que sea igual al desplazamiento horizontal de la lenteja desde el punto más bajo de la oscilación. La distancia vertical desde el origen no representará la distancia vertical de la lenteja desde ningún sitio; en cambio, podemos elegir darle el mismo valor numérico que la velocidad de la lenteja (positiva cuando la lenteja se mueve hacia la derecha y negativa cuando la lenteja se mueva hacia la izquierda). El atractor del reloj al que no se da cuerda será entonces un único punto del plano (el origen) que representa el estado de reposo.".

Ahora, analicemos con el modelo lo que dice Lorenz. De manera sencilla, para ver el atractor de un movimiento oscilatorio amortiguado, se debe graficar la velocidad en función del desplazamiento. Como este modelo implica el empleo de una rotación alrededor del punto de apoyo, las variables a representar serán angulares. La gráfica obtenida es la siguiente:

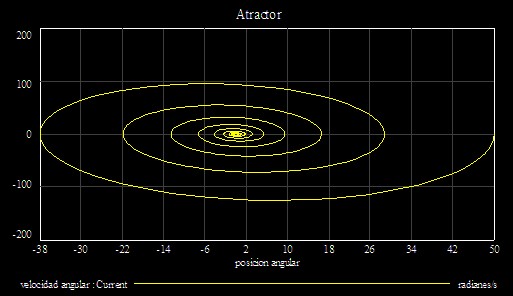
y resulta evidente que la espiral resultante converge a un punto de posición cero, con velocidad cero; es decir, el punto de equilibrio o atractor.

Pero con este modelo podemos analizar también que sucede con el atractor de un péndulo forzado. Cambiando el valor de F(t) y haciendo la simulación, la gráfica obtenida es la siguiente:

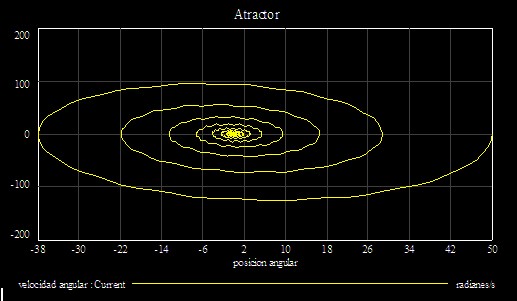
donde se ve que la trayectoria es más errática que en el caso anterior, pero el comportamiento es el mismo.

Y nos queda una última pregunta: ¿qué sucede si el péndulo es armónico simple?. Para nuestro modelo, aparte de F(t), b es igual a cero. No hay amortiguamiento. "El atractor de un péndulo de reloj al que se le dé cuerda siempre será una superficie cerrada, parecido a una elipse.... Sin importar la rapidez que le imprimamos al péndulo al comenzar su oscilación, pronto adquirirá su comportamiento normal y, entonces, cuando oscile hacia la derecha, el punto que representa su estado se moverá hacia la derecha a lo largo de la mitad superior o positiva del círculo cruzando el punto más alto cuando la lenteja consigue su máxima celeridad. Mientras el péndulo oscila de vuelta hacia la izquierda, el punto retrocederá por la mitad inferior o negativa del círculo, después de lo cual continuará sus circuitos en el sentido de las agujas del reloj". (Pág. 43).

Volvamos a comprobar lo que dice Lorenz, mediante la siguiente gráfica:

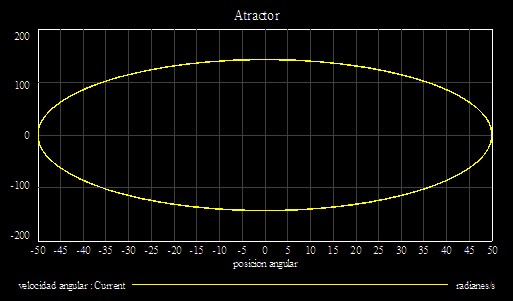
Pues bien, el modelo también permite ver que no hay atractor, y la gráfica de la velocidad angular en función de la posición angular es una elipse. Además, es un sistema no disipativo porque este péndulo se mantiene en movimiento mediante la maquinaria del reloj contra los amortiguadores del rozamiento; por lo tanto, no es amortiguado ni forzado. Los sistemas en los que los volúmenes de los espacios de fase, o áreas si el sistema tiene dos variables - como en este caso - ni disminuyen ni se incrementan con el tiempo, se llaman conservadores de volumen. Los sistemas en los que alguna magnitud, como por ejemplo la cantidad total de energía, mantiene un valor fijo con el paso del tiempo se llaman conservadores. El conservadurismo y la conservación del volumen muchas veces van "de la mano", y los sistemas que presentan ambas propiedades se conocen como hamiltonianos. Los modelos de sistemas físicos reales bien conocidos que se limitan a "pasar por alto" todos los procesos disipativos son generalmente hamiltonianos. Como en el caso del péndulo armónico simple, los conjuntos de puntos extendidos en el espacio de fase no convergerán en conjuntos de menor tamaño, y no habrá atractores.

Conclusiones: En este trabajo he presentado una propuesta para emplear el modelo de los Movimientos Oscilatorios en la introducción de conceptos sobre la Teoría del Caos. Si bien se trata de un resumen, queda demostrado ampliamente que se pueden presentar numerosos conceptos sobre el caos, tales como espacio de fase; atractor; sistemas disipativos; sistemas hamiltonianos; entre otros temas, anteriores y posteriores.

Además, estoy convencido que se deben enseñar en las Universidades conceptos sobre las nuevas disciplinas y concepciones del mundo: no se pueden seguir dando siempre los mismos marcos teóricos en la gestión del conocimiento, cuando es evidente en el mundo actual la presencia de nuevos y complejos desafíos intelectuales en la resolución de problemas.

Tampoco debemos olvidarnos que una herramienta fundamental en la mencionada gestión del conocimiento es la Dinámica de Sistemas. De hecho, y de acuerdo a mi experiencia personal, el haber creado un modelo sobre sistemas oscilantes me ha permitido trabajar con un amplio espectro en la Física Clásica, con el estudio de variables cinemáticas, dinámicas y energéticas simultáneamente; y ahora, con términos propios de la Teoría de Caos. El aprovechamiento intelectual que se puede hacer con estos tipos de modelos superan los límites y la imaginación; y es una gran noticia que así sea.

(*) Puede solicitar información más detallada de este trabajo al autor

---