Fibonacci (o Leonardo Pisano) fue un matemático que vivió parte de su vida en Pisa (Italia) entre 1170 y 1250. Se decía de él que era un hombre dedicado a resolver cuestiones que no tenían valor práctico. En una oportunidad, se le planteó el siguiente problema:
"En un patio cerrado, se coloca una pareja de conejos para ver cuántos descendientes produce en el curso de un año, y se supone que cada mes a partir del segundo mes de su vida, cada pareja de conejos da origen a una nueva. Calcular la cantidad de parejas de conejos al cabo de un año"
La solución del problema dio lugar a una sucesión de números que se hizo célebre y se conoce como Sucesión de Fibonacci. En ella, cada término resulta de la suma de los dos anteriores. De este modo, partiendo de 1 será: 1,1,2,3,5,8..... Estos números dan la cantidad de parejas de conejos a medida que pasan los meses.
La curiosidad de saber si era posible reproducir esa situación mediante un modelo dio lugar al presente trabajo, que probablemente no tenga ningún valor práctico.
El modelo:
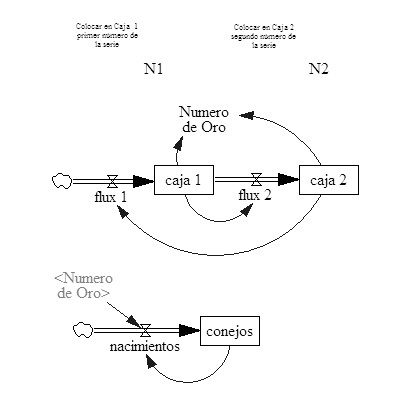
Es extremadamente sencillo y consta de dos flujos, Flux 1 y Flux 2, dos niveles, Caja 1 y Caja 2 y dos variables auxiliares, N1 y N2, que permiten cambiar los valores iniciales de Caja 1 y Caja 2. Sin embargo, no es tan sencillo entender porque en C1 y F2 se genera una sucesión de Fibonacci.
Un análisis de cómo trabaja el software permite entenderlo.
Simplificando la nomenclatura, y haciendo Flux 1 = F1, Flux 2 = F2, Caja 1 = C1 y Caja 2 = C2, y trabajando estas variables como variables con subíndices que hacen referencia al tiempo, tendremos los valores de arranque:
t= 0 F1(0) = 1 C1(0) = 1 F2(0) = 1 C2(0) = 1
Veamos en t = 1 y t= 2
t= 1 F1(1) = 2 C1(1) = 1 F2(1) = 1 C2(1) = 2
t= 2 F1(2) = 3 C1(2) = 2 F2(2) = 2 C2(2) = 3
Del diagrama del modelo podemos ver que F1 = C2 y que F2 = C1. Ademas, que en cualquier instante t el valor del flujo y del nivel que define ese valor son el mismo, así por ejemplo F1(1)=C2(1) = 2 y F2(1)=C1(1)=1. Pero también debemos recordar que el valor de un dado nivel a un dado tiempo resulta de sumar el valor que tenía en el tiempo anterior, mas los ingresos menos los egresos en el tiempo anterior.
Así que para un tiempo cualquiera n tendremos
t=n F1(n) = C2 (n)
C1(n) = C1(n-1) + F1(n-1) - F2(n-1)
F2(n) = C1 (n)
C2(n) = C2(n-1) + F2(n-1)
Sustituyendo F1 y F2 en términos de C1 y C2 y simplificando obtenemos:
(1) C1 ( n) = C2 (n-1)
(2) C2 (n) = C2 (n - 1) + C1 (n -1)
Trabajando sobre la ec (2), resulta que
(3) C2(n-1) = C2 (n-2) + C1(n-2)
Pero C2(n-2) = C1 (n-1) así que reemplazando todo en (1)
C1(n) = C1 (n - 1) + C1 (n - 2)
Que es precisamente lo que hace la sucesión de Fibonacci, es decir, cada nuevo término resulta de la suma de los dos anteriores. Y de ahí que en la Caja 1 (y en realidad en todas las variables) aparece la sucesión.
Pero avancemos más: si se efectúa el cociente entre cada término y el anterior, puede verse que la correspondiente sucesión converge al Número de Oro, cuyo valor es 1.618034.
Ahora bien: ¿será posible resolver el problema planteado a Fibonacci mediante un modelo de dinámica poblaciónal?
La segunda parte del modelo da la solución. Simplemente, si utilizamos el cociente calculado en Número de Oro como tasa de crecimiento vegetativo, obtenemos el mismo resultado que Fibonacci.
Dando valores enteros a N1 y N2 (preferiblemente N1 < N2) , puede experimentarse el comportamiento del modelo.
Según Wikipedia la dinámica de sistemas es una técnica para analizar y modelar el comportamiento temporal en entornos complejos. Se basa en la identificación de los bucles de realimentación entre los elementos, y también en las demoras en la información y materiales dentro del sistema. Lo que hace diferente este enfoque de otros usados para estudiar sistemas complejos es el análisis de los efectos de los bucles o ciclos de realimentación, en términos de flujos y depósitos adyacentes. De esta manera se puede estructurar a través de modelos matemáticos la dinámica del comportamiento de estos sistemas. La simulación de estos modelos actualmente se puede realizar con ayuda de programas computacionales específicos.
Originalmente desarrollada en 1950 para ayudar a los administradores de empresas a mejorar su comprensión de los procesos industriales, actualmente se usa en el sector público y privado para el análisis y diseño de políticas. Fue creada a principios en la década de 1960 por Jay Forrester de la MIT Sloan School of Management del Massachusetts Institute of Technology) con la creación del MIT System Dynamics Group.
Los modelos de simulación con Dinámica de Sistemas tienen aplicaciones en prácticamente todas las áreas del conocimiento como podemos observar en los numerosos artículos publicados en los congresos anuales de la System Dynamics Society. Se trata de una potente herramienta para:
Enseñar a los reflejos del sistema de pensamiento de las personas que está siendo entrenado.
Analizar y comparar los supuestos y modelos mentales acerca de cómo funcionan las cosas.
Obtener una visión cualitativa sobre el funcionamiento de un sistema o las consecuencias de una decisión.
Reconocer arquetipos de sistemas disfuncionales en la práctica diaria.
Los modelos permiten simular el impacto de diferentes políticas relativas a la situación a estudiar ejecutando simulaciones what if (¿qué pasaría si?) que permiten ver las consecuencias a corto y medio plazo, y ser de gran ayuda en la comprensión de cómo los cambios en un sistema lo afectan en el tiempo. En este sentido es muy similar al Pensamiento sistémico ya que se basa en los mismos diagramas de causales con bucles o lazos de retroalimentación (feedback). Sin embargo, estos modelos de simulación permiten además hacer simulaciones para estudiar el comportamiento de los sistemas y el impacto de políticas alternativas. Se utiliza en especial para investigar la dependencia de los recursos naturales y los problemas resultantes del creciente consumo a nivel global para mejorar el especial en el desarrollo de nuevos productos. Existe una gran variedad de marcas de software en el mercado que ayudan a aplicar esta herramienta de una forma amigable: Vensim, Stella, ithink, Powersim, Dynamo, etc.
(*) Puede solicitar información más detallada de este trabajo al autor
