La llegada del verano desata las crisis de sobrepeso. Veamos a continuación un análisis de este proceso.

Describimos el problema, en forma de relaciones causales

A mayor sobrepeso mayor será la talla del pantalón (positiva) y a mayor talla de pantalón menor es el ánimo (negativa). Y cuando menor es el ánimo mayores son las ganas de comer para mitigar la ansiedad (negativa) y si aumentan las ganas de comer, aumenta el sobrepeso (positiva). Al final obtenemos un bucle positivo:

Sobrepeso - Talla pantalón - Ánimo - Comer - Sobrepeso

Identificamos los Niveles

Tenemos diversos niveles: el peso y la talla del pantalón. Sin embargo, podrían considerarse niveles más abstractos, es decir donde no tenemos unidades físicas, como pudiera ser el ánimo.

Identificamos los Flujos

Siguiendo con el problema del sobrepeso, un flujo puede ser el comer, que podría medirse en gramos/día o en calorías/día. Dependiendo del modelo que podamos idear, también podríamos suponer un flujo que se acumularía en la talla del pantalón, que se puede llamar algo como "tasa de engorde" que se puede medir en cm/semana o mm/día.

Identificamos las Variables Auxiliares

Una variable auxiliar es el sobrepeso que mide la diferencia entre el peso actual y el peso ideal. Otra puede ser el estado de ánimo (aunque bien pudiera ser un nivel como hemos considerado anteriormente) como una variable que transforma la talla del pantalón en "velocidad" de engorde. Otras variables auxiliares constantes pueden ser el peso ideal o algún coeficiente que pudiéramos añadir para ayudar a ajustar las unidades como coeficiente de hambre en función del desánimo.

Dibujamos el Diagrama Causal

Después de la reflexión de las últimas cuestiones, al diagrama causal hemos añadido la variable Peso y una variable exógena de objetivo, Peso Ideal. Por lo quedaría el siguiente Diagrama Causal:

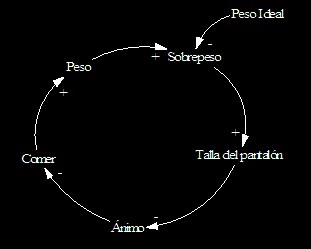
Dibujamos el Diagrama de Forrester

Con todas las limitaciones (porque las personas también adelgazan y porque el desánimo tiene un límite) proponemos el siguiente Diagrama de Forrester, donde han surgido una serie de coeficientes con la necesidad de ajustar las unidades. El Peso se mide en gramos y la Talla en centímetros. La constante exógena, Peso ideal (gr) nos indica cuál es peso en el cual una persona se siente feliz, y la variable auxiliar Sobrepeso (gr) nos mide la discrepancia entre el Peso real y el Peso Ideal.

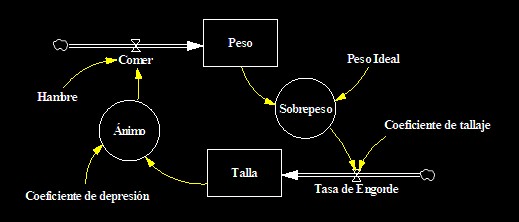El flujo Tasa de Engorde (cm/día) nos indica cómo va creciendo la talla del pantalón por día y el Coeficiente de tallaje (cm/(gr.día)) que nos relaciona el sobrepeso con la talla. El Ánimo es una variable auxiliar abstracta, en este caso nos inventamos unas unidades, unidades_de_ánimo, un valor bajo nos debería indicar que la persona está muy deprimida, al borde del suicidio, y un valor elevado nos indicará un estado eufórico. Para ajustar las unidades, necesitamos un Coeficiente de depresión (unidades_de_ánimo/cm) que nos indicará cuán animada o deprimida está la persona en función del tamaño de su cintura. Finalmente, como hemos comentado anteriormente, Comer es un flujo (gr/día) que nos indica cuántos gramos engorda por día. Esto es una simplificación, es decir nos indica lo que engorda, no lo come.

Para ajustar las unidades necesitamos un coeficiente que he llamado Hambre (gr/(unidades_de_ánimo·dia)) que nos dice cuanto necesita comer al día para mitigar la ansiedad. Independientemente de la adecuación del modelo a la realidad, pues sólo es un modelo bastante apriorístico, podemos encontrarnos con disparates como que una persona muy deprimida puede llegar a engordar, por ejemplo, más diez kilos en un día, esto nos sugiere que debería existir algún bucle de autorregulación. Igualmente una persona no puede desanimarse infinitamente o bien se suicida o bien acude a un médico; o cuando una persona tiene mucha tripa, no aumenta constantemente su talla del pantalón, simplemente se lo ajusta por debajo de la barriga (apareciendo esas famosas "barrigas cerveceras"). En cualquier caso, ha sido una buena reflexión sobre la importancia del ajuste y coherencia de las unidades apareciendo tres coeficientes: Coeficiente de tallaje (cm/(gr.día)), Coeficiente de depresión (unidades_de_ánimo/cm) y Hambre (gr/(unidades_de_ánimo·dia)).

Según Wikipedia la dinámica de sistemas es una técnica para analizar y modelar el comportamiento temporal en entornos complejos. Se basa en la identificación de los bucles de realimentación entre los elementos, y también en las demoras en la información y materiales dentro del sistema. Lo que hace diferente este enfoque de otros usados para estudiar sistemas complejos es el análisis de los efectos de los bucles o ciclos de realimentación, en términos de flujos y depósitos adyacentes. De esta manera se puede estructurar a través de modelos matemáticos la dinámica del comportamiento de estos sistemas. La simulación de estos modelos actualmente se puede realizar con ayuda de programas computacionales específicos.

Originalmente desarrollada en 1950 para ayudar a los administradores de empresas a mejorar su comprensión de los procesos industriales, actualmente se usa en el sector público y privado para el análisis y diseño de políticas. Fue creada a principios en la década de 1960 por Jay Forrester de la MIT Sloan School of Management del Massachusetts Institute of Technology) con la creación del MIT System Dynamics Group.

Los modelos de simulación con Dinámica de Sistemas tienen aplicaciones en prácticamente todas las áreas del conocimiento como podemos observar en los numerosos artículos publicados en los congresos anuales de la System Dynamics Society. Se trata de una potente herramienta para:

Enseñar a los reflejos del sistema de pensamiento de las personas que está siendo entrenado.

Analizar y comparar los supuestos y modelos mentales acerca de cómo funcionan las cosas.

Obtener una visión cualitativa sobre el funcionamiento de un sistema o las consecuencias de una decisión.

Reconocer arquetipos de sistemas disfuncionales en la práctica diaria.

Los modelos permiten simular el impacto de diferentes políticas relativas a la situación a estudiar ejecutando simulaciones what if (¿qué pasaría si?) que permiten ver las consecuencias a corto y medio plazo, y ser de gran ayuda en la comprensión de cómo los cambios en un sistema lo afectan en el tiempo. En este sentido es muy similar al Pensamiento sistémico ya que se basa en los mismos diagramas de causales con bucles o lazos de retroalimentación (feedback). Sin embargo, estos modelos de simulación permiten además hacer simulaciones para estudiar el comportamiento de los sistemas y el impacto de políticas alternativas. Se utiliza en especial para investigar la dependencia de los recursos naturales y los problemas resultantes del creciente consumo a nivel global para mejorar el especial en el desarrollo de nuevos productos. Existe una gran variedad de marcas de software en el mercado que ayudan a aplicar esta herramienta de una forma amigable: Vensim, Stella, ithink, Powersim, Dynamo, etc.

(*) Puede solicitar información más detallada de este trabajo al autor

---