Simulación dinámica del valor local de la Gravedad (g)
Basado en un modelo de simulación con Vensim
Coria Hanne D. – Velazco Angela del C. - Navarro Silvia Inés
Juarez Gustavo Adolfo – Leguizamón Guillermo N.
Facultad de Ciencias Exactas y Naturales – Universidad Nacional de Catamarca
bio@matematica.net.ar
INTRODUCCION
El aprendizaje por descubrimiento es una metodología fundamental en la comprensión de los fenómenos científicos, aporta una visión práctica y fomenta la adquisición de habilidades aplicadas, que una enseñanza puramente teórica no puede suplir, así los entornos de aprendizaje basados en el modelado matemático y la simulación son uno de los más utilizados en las áreas científico-tecnológicas para adquirir este tipo de aprendizaje. Para ello se propuso la realización de un trabajo práctico de características motivadoras, que integra un conjunto de magnitudes y leyes físicas, aprovechando las ventajas que nos brindan los modelos de dinámica de sistemas en la modalidad de criterios de valoración para la adquisición y procesamiento de datos.
El objetivo fue determinar el valor de gravedad local, por medio de un péndulo simple que describe un movimiento armónico simple en torno a su posición de equilibrio con una precisión prefijada.
Destacamos que la atracción de la tierra no es una constante en todos los puntos de la superficie de ésta, para nuestro caso el valor de la gravedad que obtuvimos fue determinado en la provincia de Catamarca ubicada en la Región Noroeste de la República Argentina, siendo sus límites: al Norte la provincia de Salta; al Este las provincias de Tucumán y Santiago del Estero; al Sur Córdoba y La Rioja; y al Oeste la República de Chile por medio de la Cordillera de los Andes. Tiene una superficie de 102.602[km2], y su ubicación astronómica aproximada es: entre los 25° 12' y 30° 40' de latitud Sur y desde los 64° 55' hasta los 69° 28' de longitud Oeste.
EL PENDULO SIMPLE Y LA GRAVEDAD
El valor estándar de la gravedad corresponde a un punto ubicado justo sobre el ecuador , en el cual la aceleración de la gravedad varía dependiendo de la latitud y la elevación debido a la forma y rotación de la Tierra.
En nuestro caso específico para el cálculo de la gravedad local, utilizamos un péndulo simple de longitud cuyo hilo no puede considerarse un cuerpo rígido ya que la distribución de masa del péndulo se lo puede tomar invariable, si el hilo no cambia de longitud a lo largo del movimiento. Al separarlo de su posición de equilibrio oscila alrededor de dicha posición con un período T , es decir que en uno por segundos se repite el movimiento generándose una oscilación completa, describiéndose un ángulo de pequeña oscilación sin rozamientos En este método dinámico, tenemos la ventaja de fijar de antemano el error con que queremos encontrar nuestra magnitud, habitualmente dado en términos relativos.
Por propiedades de convergencia, se puede hacer un truncamiento en cualquier término, para obtener que la suma hasta ese término sea mayor que la suma de los restantes. Así, despreciando a partir del tercer término de la ecuación obtenemos como calcular el valor de dependiendo de la menor amplitud, la longitud y del periodo de oscilación.
Por lo tanto, la longitud del hilo se mantiene constante durante el experimento, se destaca que a partir del momento en que el péndulo oscila regularmente respecto a una pequeña amplitud se cuenta oscilaciones completas respecto a la máxima separación de equilibrio, poniéndose inmediatamente en marcha el cronómetro. El período del péndulo es de con el radio de la esfera . Asimismo se tuvo en cuenta el análisis cuantitativo del error introducido por el proceso de medición y por la característica del modelo usado, obteniéndose en la simulación el valor local igual respecto a las variables climatológicas.
MODELO DINAMICO DEL VALOR DE GRAVEDAD (g)
Para simular el valor de la gravedad partimos de valores experimentales realizados en laboratorio. Para ello, contamos con la medida de la longitud del hilo sobre la que se cuelga un peso de valor despreciable. A partir de cierto instante, se comienzan a medir los ángulos que tienden a un valor de equilibrio registrándose los valores angulares y de ellos se calcula el periodo , tales datos se los coloca en tablas, que en la simulación se indican con tabla3 a los periodos calculados y tabla2 a los valores angulares medidos. De esta manera se va obteniendo el valor de la gravedad experimental.
La simulación cuenta con valores de calculados de acuerdo a los ángulos medidos y se los colocan en la tabla1, a fin de hallar el valor de la gravedad que llamamos gravedad simulada el cual depende de los mismos valores angulares dados en tabla2, agregándose un factor de error proveniente de errores de medición y que indicamos con la variable error. La cual ésta fue definida con por lo que en Vensim se la escribió como (-1)^Time*0.0002 .
Por otro lado y con el fin de comparar gráficamente los valores experimentales y simulados de la gravedad se insertan una variable auxiliar que refleja el valor estándar de la gravedad.
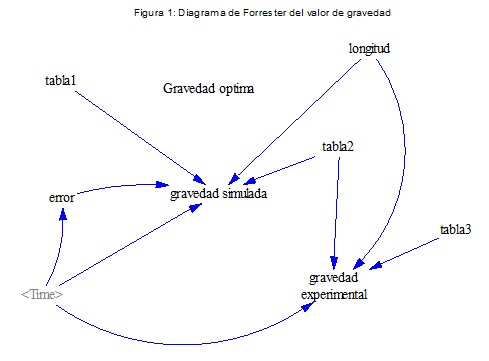
De lo expresado presentamos el diagrama de Forrester (figura 1) que determina el valor aproximadolocal obtenido a partir de ecuación (2).
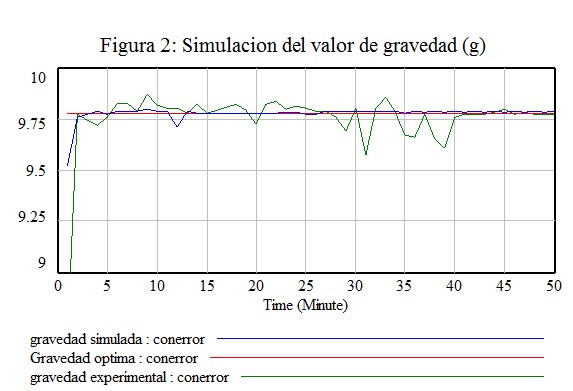
En la figura 2, se muestra la simulación obtenida del valor muy cercano al resultado teórico que se señala en los libros de Física, permitiéndonos establecer cierta aproximación entre el valor teórico y el simulado.
CONCLUSION
El desarrollo de éste experimento permito que los alumnos adquieran una mejor comprensión del método científico verificando la validez de los desarrollos teóricos, a partir de la comparación entre el valor experimental y el valor simulado de la gravedad del lugar a través de las condiciones preestablecidas en el modelo matemático que se determina por medio de la Dinámica de Sistemas con la simulación correspondiente.
BIBLIOGRAFIA
Maiztegui A.- Gleiser R. (2000). Mediciones de Laboratorio. Editorial Talleres Gráficos de José Solsona
Martín García Juan (2000). Creación de Modelos en Ecología. Cátedra UNESCO a la UPC. Manual Vensim Ple 3.1
Serway, F. (5º Edición 2001). Física. Editorial Prentice-Hall
Solaz Portolés J. J. y Sanjosé López, V. (1992). El papel del péndulo en la construcción del paradigma Newtoniano. Enseñanza de las Ciencias, 10 (l), 95-100.
Martín García Juan (2004). Sysware. Edición del Autor. Barcelona.
Martín García Juan (2008). Ejercicios Avanzados en Dinámica de Sistemas. Edición del Autor. Barcelona.
(*) Puede solicitar información más detallada de este trabajo al autor
|
