Perfil de las manifestaciones de la fuerza aplicada en el deporte.
Estudio basado en un modelo de Dinámica de Sistemas

Salvador Olaso
solaso@inefc.udl.cat
José Vicente Beltrán Garrido
josevicentebelga@msn.com

1. Introducción

A partir de la posición de la Física y de la Fisiología y siguiendo el patrón general de la ciencia, conocemos como las relaciones que existen entre las variables que intervienen en un problema, constituyen el instrumento explicativo por excelencia a la hora de analizar los fenómenos. La idea de que una variable depende de otra es, pues, una de las nociones básicas del conocimiento científico. Del mismo modo conocemos como la expresión analítica de un modelo se logra a partir de una o varias funciones, lo cual no es más que el recurso matemático empleado para indicar la existencia de una relación cualquiera entre variables. De esta manera, para indicar que una variable depende de otra, se dice que una es función de la otra.

La representación simbólica de las funciones tiene una formulación general empleada de la manera siguiente: y = f (x)

Donde el símbolo f, además de indicarnos que existe relación o dependencia entre x e y, nos informa que, si se formalizara la relación funcional cuantitativamente mediante una ecuación, dados los valores de x –variable explicativa, independiente- podríamos obtener valores correspondientes de y -variable explicada, dependiente- simplemente sustituyendo los primeros en la ecuación.

Anunciamos que la función que liga las variables x e y es directa o creciente cuando a un incremento/decremento de la primera le corresponde un incremento/decremento de la segunda. Contrariamente, se calificará como inversa o decreciente cuando el signo de los cambios sea contrario, o sea, cuando a una variación positiva de x se le asocie una variación negativa de y.

Por lo tanto, la función lineal es la representación teórica más simple que puede adoptar la relación entre dos variables. Partiendo de la sistémica y aplicándola al entrenamiento deportivo se plantea un nuevo modelo para evaluar el Perfil de las Manifestaciones de la Fuerza (PMF) de un deportista cualquiera.

2. El Perfil de las Manifestaciones de la Fuerza.

El PMF se obtiene a través de la suma de las diferentes alturas alcanzadas por el centro de gravedad del sujeto, en cada salto de la batería del test de Bosco, y los índices derivados de los mismos (saltos). El PMF queda definido a partir de la batería siguiente:

PMF = SJ100 + (SJ – SJ100) + (CMJ – SJ) + (ABK – CMJ) + (DJ – ABK)

A continuación se describe cada parámetro:

• SJ100 > Squat Jump ejecutado con una sobrecarga del 100% del peso corporal.

• SJ > Squat Jump, salto sin contramovimiento.

• CMJ > Countermovement Jump, salto con contramovimiento.

• ABK > Abalakov, salto con contramovimiento e impulso de los brazos.

• DJ > Drop Jump, salto hacia abajo desde una altura determinada, para la obtención del PMF siempre se utiliza el DJ con mejor índice de reactividad, al que se le denominará Mejor DJ, que viene determinado con el índice de reactividad, expresado como el cociente existente entre la altura de caída del salto (hc) y la altura alcanzada por el centro de gravedad del sujeto durante el salto (hv), por tanto el índice de reactividad será igual a hc/hv.

El PMF que se forma es resultado de la conjugación de todos los saltos de la batería y los índices que se derivan, cada parámetro tendrá su proporción de importancia, según la capacidad de salto del sujeto evaluado. La representación porcentual del PMF quedaría de la siguiente manera:

100% = A% + B% + C% + D% + E%

• A% = SJ100 > Capacidad Contráctil, cualidad que posee el músculo para manifestar fuerza a través del aparato contráctil muscular.

• B% = SJ – SJ100 > Capacidad de Reclutamiento Instantáneo y Sincronización, cualidad que posee el músculo para manifestar fuerza a través de la activación voluntaria de elevado número de fibras musculares organizadas.

• C% = CMJ – SJ > Capacidad Elástica, contribución de la energía elástica en la altura de vuelo alcanzada por el de gravedad del sujeto.

• D% = ABK - CMJ > Capacidad de Utilización de Brazos ó Índice de Utilización de los Brazos (IUB), contribución de la coordinación de los brazos en la altura de vuelo alcanzada por el centro de gravedad del sujeto.

• E% = DJ - ABK > Capacidad Refleja, contribución del reflejo miotático y los órganos de Golgi en la altura de vuelo alcanzada por el centro de gravedad del sujeto.

Los saltos de la batería del test de Bosco -variables auxiliares primarias-, y los índices derivados -variables auxiliares secundarias-, de los resultados de los test conforman el PMF del deportista -núcleo central del sistema: nivel-.

3. Determinado el Perfil de las Manifestaciones de la Fuerza (PMF). El modelo.

Teóricamente ideal para una disciplina deportiva, introducimos una Previsión de PMF, que será nuestro objetivo a conseguir. A partir de aquí podemos observar la diferencia existente entre el PMF de nuestro atleta y el PMF ideal, además de poder observar el efecto que tienen distintas manipulaciones de los parámetros sobre el PMF, de esta manera se puede decidir en que parámetro incidir, para conseguir el objetivo final.

El estudio de las ecuaciones nos debe revelar el complemento entre todos los subconjuntos, representados por los diferentes saltos de la batería del test de Bosco -que a su vez representan un tipo diferente de manifestación de la fuerza de las extremidades inferiores-, donde el PMF del deportista cambia en función de los valores obtenidos en cada salto, de manera que se aproxima en mayor o menor medida –Déficit- al PMF ideal para la disciplina deportiva -%PMF Previsto-. Observando la diferencia entre el PMF realizado y el PMF ideal podremos reorientar el entrenamiento en función de las necesidades del momento.

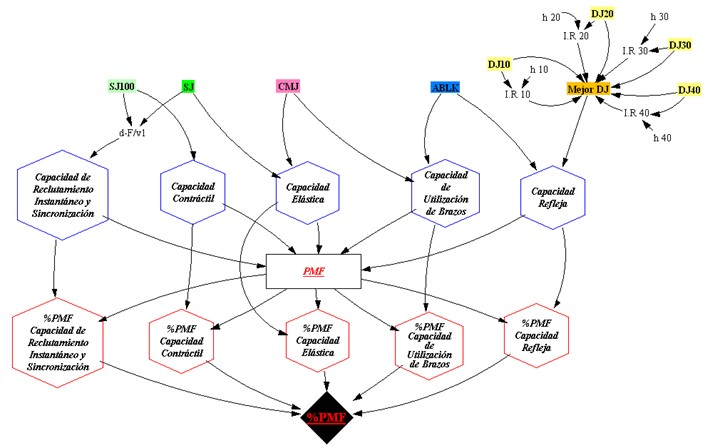
FIGURA 1. Modelo de dinámica de sistemas (DS) del Perfil de las Manifestaciones de la Fuerza (PMF).

4. Simulación del modelo.

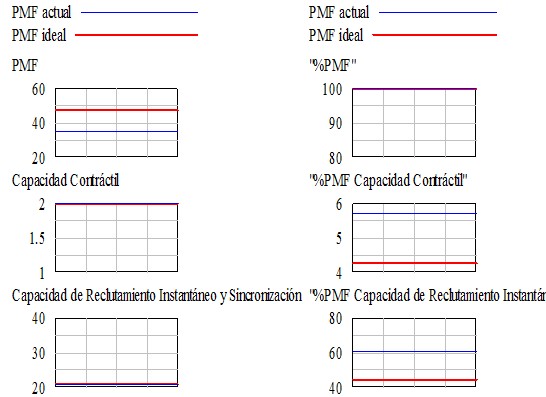
FIGURA 2. Gráficas de los valores absolutos (izquierda) y relativos (derecha) del PMF ideal (rojo) y el PMF inicial (azul), atletas simulados.

5. Valoración del modelo y simulaciones.

En las ecuaciones del modelo, los valores que adquiere cada constante para determinar el PMF ideal y el PMF actual. En las gráficas se dibujan las funciones lineales debido a que se trata de observaciones transversales del sujeto y no de prever las evoluciones de los parámetros a lo largo del tiempo –otro tipo de análisis a ilustrar en otra ocasión-.

Las gráficas ubicadas en la columna de la izquierda, representan los valores absolutos que adquiere cada parámetro del PMF, mientras que las gráficas de la derecha, adquieren los valores relativos para cada parámetro del PMF. En la primera de la izquierda se puede apreciar que el valor absoluto del PMF ideal –rojo- y actual –azul-, son de 57 y 35 respectivamente, mientras que en la primera de la derecha, al tratarse de valores relativos, ambos PMF adquieren un valor del 100%. En los gráficos expuestos (Figura 2), se muestra la comparación que se puede establecer entre el PMF actual -en color rojo, en el caso de un saltador de longitud que aspira a conseguir una buena posición en el ranking nacional-, y el PMF ideal -en azul-, que nos indica el PMF que ya posee, de manera hipotética, el actual líder del ranking de salto de longitud. El PMF ideal es aquel al que tiende el atleta a partir de la eficacia del entrenamiento, y es un dato a tener en cuenta para el entrenador, ya que la comparación de ambos PMF permite intuir qué tipo de mejoras debe realizar para lograr el objetivo. Por lo tanto, observando las diferencias existentes entre ambos parámetros del PMF, se orienta el proceso de entrenamiento (Tablas 1, 2, 3).

En la simulación del modelo, se ha variado el valor del DJ30, que ha pasado de un valor de 57 cm. -que lo tomaríamos como el valor del DJ del atleta ideal-, ha valer 35 cm -que sería el valor que le corresponde al atleta líder-, de ahí que se observen claramente las diferencias entre un PMF y otro.

Por otra parte, también se puede representar la evaluación de un mismo sujeto al principio -color azul-, y al final -color rojo-, de un periodo de entrenamiento, siendo esta una manera objetiva de realizar evaluaciones transversales de nuestros atletas. De esta manera, el cambio observado en las gráficas, permite comprobar si los cambios producidos son los que realmente se buscaban con el entrenamiento realizado, en este caso se ha conseguido un aumento significativo del DJ30, que pasa de tener un valor de 35 cm a un valor de 57 cm.