Modelos de Simulacion. Vensim. Dinamica de Sistemas. Modelos de Simulacion. Vensim. Dinamica de Sistemas. Modelos de Simulacion. Vensim. Dinamica de Sistemas. Vensim.

Boletín de Dinámica de Sistemas

Análisis de la producción de alcohol mediante levaduras

Basado en un modelo de simulación con Vensim

Rafael Emilio Avendaño
alinka912000@yahoo.com.mx



Tenemos a disposición una sustancia fermentable por levaduras y dos tipos de levaduras llamémoslas "levadura A" y "levadura B" con propiedades bien definidas a saber: La levadura A tiene un crecimiento lento y produce relativamente poco alcohol. La levadura B crece deprisa y produce mucho alcohol, deseamos una cierta cantidad de alcohol en un determinado tiempo.

Alcohol: Está en función de la producción unitaria de alcohol por tipo de levadura.

Producción de alcohol por tipo de levadura: Está en función de la producción unitaria de cada levadura y del tipo de levadura

Levadura: Está en función de su velocidad de crecimiento.

Concentración de alcohol: Está en función de la cantidad de alcohol deseado y del alcohol obtenido por unidad de levadura en un determinado período de tiempo

El modelo debe de ayudarnos a elegir la cantidad más adecuada de cada tipo de levadura para los fines perseguidos: Obtener una cierta cantidad de alcohol en un determinado tiempo.

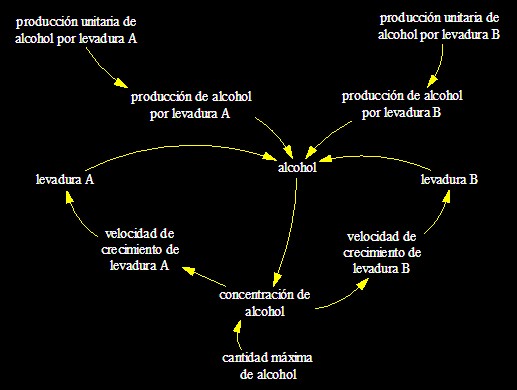
PRODUCCIÓN DE ALCOHOL MEDIANTE LEVADURAS

Diagrama Causal

Tiene dos áreas de incidencia: Producción de alcohol y el comportamiento de cada tipo de levadura. El tránsito del Diagrama Causal al Diagrama de flujos es necesario para poder trabajar en el ordenador, no es proceso automático, con frecuencia se requiere crear nuevos elementos como flujos. Hemos definido en el Diagrama de flujos, Alcohol , como el único nivel del modelo, se puede crear otro modelo con diferente estructura.


Ecuaciones del Modelo

(01) producción unitaria de alcohol por levadura A = 0.03

units: unidades de alcohol(UA)/hora

(02) producción de alcohol por levadura B =

levadura B * producción unitaria de de alcohol por levadura B

units :UA

(03) levadura A = velocidad de crecimiento en levadura A

units :Dmnl

(04) velocidad de crecimiento en levadura A = WITH LOOKUP

(Concentración de alcohol ((0,8),(1,8),(2,8),(3,8)

units: Dmnl/hora

(05) velocidad de crecimiento en levadura B = WITH LOOKUP

(Concentración de alcohol ((0,8),(1,8),(2,8)(3,8),(5,0)(10,0))

Units :Dmnl /hora

Es función de la concentración de alcohol, según recogemos en la tabla, cuando la concentración de alcohol es 0 ,la velocidad de crecimiento es 8 y cuando la concentración de alcohol llega a 10UA ,la velocidad de crecimiento es 0

(06) producción de alcohol por levadura A =

levadura A * producción unitaria de alcohol por levadura A

Units : UA

(07) INITIAL TIME = 0

(08) FINAL TIME = 20

(09) levadura B = velocidad de crecimiento en levadura B

Units : Dmnl

(10) producción unitaria de alcohol por levadura B = 0,1

Units : UA /hora

(11) ALCOHOL = INTEG (ALCOHOL* (producción de alcohol por levadura A + producción de alcohol por levadura B )

Initial value = 20

Son las unidades de alcohol que tenemos al inicio,corresponden a una cierta cantidad en el tiempo cero (20 UA).

(12) Concentración de alcohol = ALCOHOL / alcohol máximo

Units : UA

Concentración de alcohol es la cantidad de alcohol acumulada en un determinado tiempo dividido por la cantidad de alcohol a obtener en un determinado tiempo.

(13) alcohol máximo = 150

Units = UA

Es la cantidad de alcohol deseada en un determinado período de tiempo.


Resultados

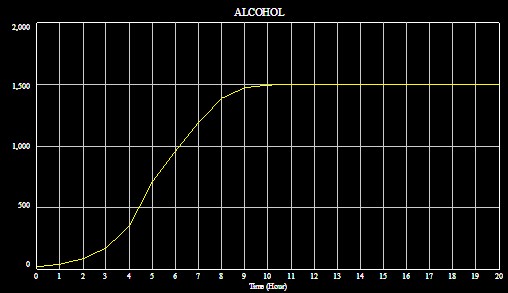
Los resultados del modelo parecen no satisfactorios


propuesta :

Debemos iniciar el proceso introduciendo ALCOHOL en el modelo, y veamos los resultados

PRODUCCIÓN DE ALCOHOL MEDIANTE LEVADURAS

Según Wikipedia la dinámica de sistemas es una técnica para analizar y modelar el comportamiento temporal en entornos complejos. Se basa en la identificación de los bucles de realimentación entre los elementos, y también en las demoras en la información y materiales dentro del sistema. Lo que hace diferente este enfoque de otros usados para estudiar sistemas complejos es el análisis de los efectos de los bucles o ciclos de realimentación, en términos de flujos y depósitos adyacentes. De esta manera se puede estructurar a través de modelos matemáticos la dinámica del comportamiento de estos sistemas. La simulación de estos modelos actualmente se puede realizar con ayuda de programas computacionales específicos.

Originalmente desarrollada en 1950 para ayudar a los administradores de empresas a mejorar su comprensión de los procesos industriales, actualmente se usa en el sector público y privado para el análisis y diseño de políticas. Fue creada a principios en la década de 1960 por Jay Forrester de la MIT Sloan School of Management del Massachusetts Institute of Technology) con la creación del MIT System Dynamics Group.

Los modelos de simulación con Dinámica de Sistemas tienen aplicaciones en prácticamente todas las áreas del conocimiento como podemos observar en los numerosos artículos publicados en los congresos anuales de la System Dynamics Society. Se trata de una potente herramienta para:

  • Enseñar a los reflejos del sistema de pensamiento de las personas que está siendo entrenado.
  • Analizar y comparar los supuestos y modelos mentales acerca de cómo funcionan las cosas.
  • Obtener una visión cualitativa sobre el funcionamiento de un sistema o las consecuencias de una decisión.
  • Reconocer arquetipos de sistemas disfuncionales en la práctica diaria.

    Los modelos permiten simular el impacto de diferentes políticas relativas a la situación a estudiar ejecutando simulaciones what if (¿qué pasaría si?) que permiten ver las consecuencias a corto y medio plazo, y ser de gran ayuda en la comprensión de cómo los cambios en un sistema lo afectan en el tiempo. En este sentido es muy similar al Pensamiento sistémico ya que se basa en los mismos diagramas de causales con bucles o lazos de retroalimentación (feedback). Sin embargo, estos modelos de simulación permiten además hacer simulaciones para estudiar el comportamiento de los sistemas y el impacto de políticas alternativas. Se utiliza en especial para investigar la dependencia de los recursos naturales y los problemas resultantes del creciente consumo a nivel global para mejorar el especial en el desarrollo de nuevos productos. Existe una gran variedad de marcas de software en el mercado que ayudan a aplicar esta herramienta de una forma amigable: Vensim, Stella, ithink, Powersim, Dynamo, etc.

    		•
    Cursos Online


    .

    Google