El movimiento de un proyectil se estudia en Mecánica como el ejemplo clásico de un movimiento bidimensional, con aceleración constante en el eje y (u ordenada) y con velocidad constante en el eje x (o abcisa). El estudio cinemático es el que generalmente se encara, y se realiza mediante dos condiciones ideales: la masa del sistema permanece constante, y se desprecia la resistencia del aire.
Esto se debe simplemente a que si fuesen empleadas dichas condiciones, el análisis del citado movimiento sería de una gran dificultad matemática, lo que "enmascararía" el significado físico del sistema a estudiar.
Debido a las limitaciones descritas en el párrafo anterior, he creado un modelo que incluye a ambas situaciones en el estudio del movimiento bidimensional mencionado, y que además permite un estudio dinámico junto al cinemático. La razón de esta última opción radica en que, por experiencia personal como docente de Física, he notado que cuando se estudian la Cinemática y la Dinámica por separado, los alumnos suelen olvidarse de que las variables velocidad y aceleración que son estudiadas en la primera, están vinculadas con la cantidad de movimiento (producto de la masa por la velocidad) y la fuerza (producto de la masa por la aceleración), respectivamente, en la segunda.
El modelo se presenta a continuación:
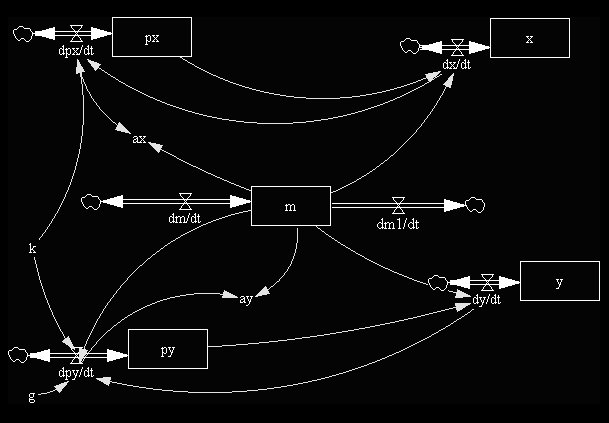
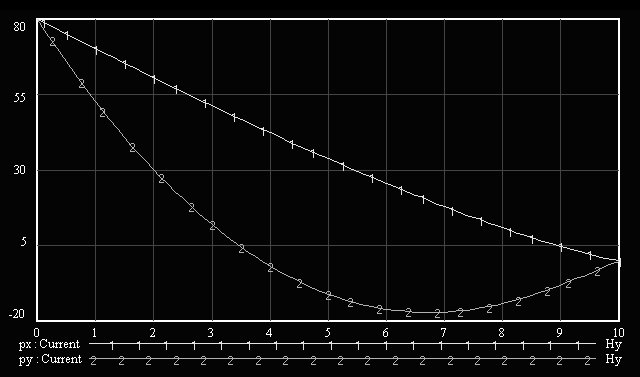
Una de las gráficas obtenidas es la siguiente, y pertenece a la cantidad de movimiento - en x e y - de un sistema que pierde su masa inicial de 2Kg a razón de 0.2 Kg/s; su cantidad de movimiento inicial es de 80 Hy (o N . s) tanto en sus componentes x e y; y tiene resistencia del aire.
El movimiento de un proyectil normalmente se define como el que realiza un móvil cuando es impulsado con una velocidad inicial, y con un cierto ángulo - mayor que 0º y menor que 90º - respecto a la horizontal.
Cuando se modifica el ángulo a 90º, y también con una velocidad inicial, el móvil describe un movimiento unidimensional conocido como "tiro vertical". Y cuando la velocidad inicial es nula, el movimiento también unidimensional es conocido como "caída libre".
Dicho de otra manera, el tiro vertical y la caída libre son casos particulares del movimiento del proyectil, debido al cambio de las condiciones iniciales. Este modelo permite no sólo analizar los movimientos citados con anterioridad como pertenecientes a la misma estructura, sino también "convencer" a quien lo emplea de que así es.
Esta última acotación está fundamentada también en mi experiencia docente, porque los estudiantes, en líneas generales, no suelen relacionar los tres tipos de movimientos mencionados.
Como conclusión, debe destacarse la polifuncionalidad de este modelo. Permite estudiar, analizar, y comprender distintos tipos movimientos tanto desde el punto de vista cinemático como dinámico de una forma relativamente sencilla; tarea que es muy difícil de realizar de otra manera. Además, los resultados suelen ser sorprendentes cuando uno realiza la simulación por primera vez en una situación que habitualmente no es tenida en cuenta cuando está acostumbrado a trabajar con las hipótesis clásicas para el movimiento del proyectil.
Según Wikipedia la dinámica de sistemas es una técnica para analizar y modelar el comportamiento temporal en entornos complejos. Se basa en la identificación de los bucles de realimentación entre los elementos, y también en las demoras en la información y materiales dentro del sistema. Lo que hace diferente este enfoque de otros usados para estudiar sistemas complejos es el análisis de los efectos de los bucles o ciclos de realimentación, en términos de flujos y depósitos adyacentes. De esta manera se puede estructurar a través de modelos matemáticos la dinámica del comportamiento de estos sistemas. La simulación de estos modelos actualmente se puede realizar con ayuda de programas computacionales específicos.
Originalmente desarrollada en 1950 para ayudar a los administradores de empresas a mejorar su comprensión de los procesos industriales, actualmente se usa en el sector público y privado para el análisis y diseño de políticas. Fue creada a principios en la década de 1960 por Jay Forrester de la MIT Sloan School of Management del Massachusetts Institute of Technology) con la creación del MIT System Dynamics Group.
Los modelos de simulación con Dinámica de Sistemas tienen aplicaciones en prácticamente todas las áreas del conocimiento como podemos observar en los numerosos artículos publicados en los congresos anuales de la System Dynamics Society. Se trata de una potente herramienta para:
Enseñar a los reflejos del sistema de pensamiento de las personas que está siendo entrenado.
Analizar y comparar los supuestos y modelos mentales acerca de cómo funcionan las cosas.
Obtener una visión cualitativa sobre el funcionamiento de un sistema o las consecuencias de una decisión.
Reconocer arquetipos de sistemas disfuncionales en la práctica diaria.
Los modelos permiten simular el impacto de diferentes políticas relativas a la situación a estudiar ejecutando simulaciones what if (¿qué pasaría si?) que permiten ver las consecuencias a corto y medio plazo, y ser de gran ayuda en la comprensión de cómo los cambios en un sistema lo afectan en el tiempo. En este sentido es muy similar al Pensamiento sistémico ya que se basa en los mismos diagramas de causales con bucles o lazos de retroalimentación (feedback). Sin embargo, estos modelos de simulación permiten además hacer simulaciones para estudiar el comportamiento de los sistemas y el impacto de políticas alternativas. Se utiliza en especial para investigar la dependencia de los recursos naturales y los problemas resultantes del creciente consumo a nivel global para mejorar el especial en el desarrollo de nuevos productos. Existe una gran variedad de marcas de software en el mercado que ayudan a aplicar esta herramienta de una forma amigable: Vensim, Stella, ithink, Powersim, Dynamo, etc.
(*) Puede solicitar información más detallada de este trabajo al autor





