El objetivo del modelo es simular el comportamiento fluídodinámico de un reactor en estado estacionario, al cual se suministra un pulso de una sustancia conocida, con el efecto de observar la respuesta de la corriente de salida.
El Caudal es igual para la corriente de entrada input como la de salida, output, y la concentración inicial es cero. A tiempo t= Tiempo inyección, aplica un pulso de Magnitud conocida y Duración igual al Time step elegido para el cálculo. La Concentración que resulta en el interior del reactor se obtiene dividiendo este input por el Volumen reactor, y es la que se transmite a la salida output.
Factor, Efecto retraso y Aplicar retraso son las variables que permiten simular situaciones diferentes en cuanto al comportamiento del reactor. Si Factor se hace uno y Aplicar retraso cero, se obtiene una respuesta muy similar a la obtenida mediante la solución exacta de la ecuación representativa, y que corresponde al reactor de comportamiento perfecto, es decir, aquel en que no hay estancamientos, y la concentración a la salida es en todo momento la misma que la interna del reactor.
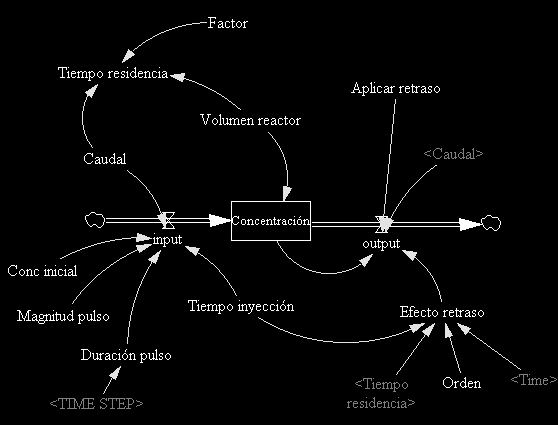Si se disminuye Factor se disminuye el volumen del reactor realmente activo, es decir, se simulan estancamientos, con lo cual el tiempo de residencia de los elementos que realmente entran y salen disminuye. Por otra parte, aplicando Efecto retraso con distintos Ordenes se representa la situación en la cual la respuesta de la corriente de salida no es inmediata porque hay un cierto retraso entre el ingreso del trazador y el comienzo de su salida.
El análisis dimensional permite obtener el T adimensional y la Distribución Edades. Esta última es una distribución de frecuencias que nos permite ver los diferentes porcentajes del trazador ingresado que van saliendo a lo largo del tiempo, e inferir el grado de apartamiento del reactor con respecto al comportamiento ideal por comparación con la respuesta para Factor=1 y Aplicar retraso = 0. Distribución Edades se acumula en Dist acum con el objeto de apreciar que cualquiera sea la situación simulada, este valor tiende a uno, puesto que es en definitiva una distribución de probabilidades aproximada, y por lo tanto el área debajo de la curva será 1.
Según Wikipedia la dinámica de sistemas es una técnica para analizar y modelar el comportamiento temporal en entornos complejos. Se basa en la identificación de los bucles de realimentación entre los elementos, y también en las demoras en la información y materiales dentro del sistema. Lo que hace diferente este enfoque de otros usados para estudiar sistemas complejos es el análisis de los efectos de los bucles o ciclos de realimentación, en términos de flujos y depósitos adyacentes. De esta manera se puede estructurar a través de modelos matemáticos la dinámica del comportamiento de estos sistemas. La simulación de estos modelos actualmente se puede realizar con ayuda de programas computacionales específicos.
Originalmente desarrollada en 1950 para ayudar a los administradores de empresas a mejorar su comprensión de los procesos industriales, actualmente se usa en el sector público y privado para el análisis y diseño de políticas. Fue creada a principios en la década de 1960 por Jay Forrester de la MIT Sloan School of Management del Massachusetts Institute of Technology) con la creación del MIT System Dynamics Group.
Los modelos de simulación con Dinámica de Sistemas tienen aplicaciones en prácticamente todas las áreas del conocimiento como podemos observar en los numerosos artículos publicados en los congresos anuales de la System Dynamics Society. Se trata de una potente herramienta para:
Enseñar a los reflejos del sistema de pensamiento de las personas que está siendo entrenado.
Analizar y comparar los supuestos y modelos mentales acerca de cómo funcionan las cosas.
Obtener una visión cualitativa sobre el funcionamiento de un sistema o las consecuencias de una decisión.
Reconocer arquetipos de sistemas disfuncionales en la práctica diaria.
Los modelos permiten simular el impacto de diferentes políticas relativas a la situación a estudiar ejecutando simulaciones what if (¿qué pasaría si?) que permiten ver las consecuencias a corto y medio plazo, y ser de gran ayuda en la comprensión de cómo los cambios en un sistema lo afectan en el tiempo. En este sentido es muy similar al Pensamiento sistémico ya que se basa en los mismos diagramas de causales con bucles o lazos de retroalimentación (feedback). Sin embargo, estos modelos de simulación permiten además hacer simulaciones para estudiar el comportamiento de los sistemas y el impacto de políticas alternativas. Se utiliza en especial para investigar la dependencia de los recursos naturales y los problemas resultantes del creciente consumo a nivel global para mejorar el especial en el desarrollo de nuevos productos. Existe una gran variedad de marcas de software en el mercado que ayudan a aplicar esta herramienta de una forma amigable: Vensim, Stella, ithink, Powersim, Dynamo, etc.
Conclusiones:
El modelo permite simular en forma sencilla distintos comportamientos, que pueden compararse contra valores prácticos obtenidos en laboratorio, e inclusive en reactores de mayor tamaño. La búsqueda del factor o del orden del retraso que mejor ajuste dará una idea de los posibles defectos constructivos que alejan al reactor del comportamiento perfecto.
(*) Si lo desea puede solicitar información más detallada al autor
